
Question and Answers Forum
Question Number 121602 by benjo_mathlover last updated on 09/Nov/20
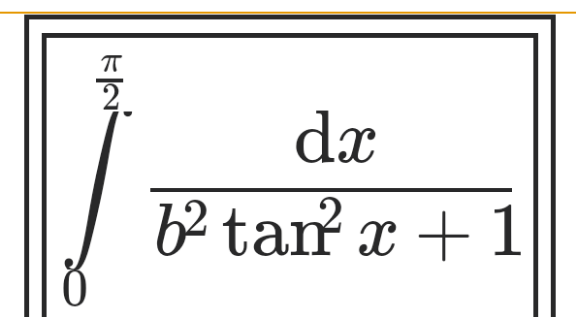
Answered by liberty last updated on 10/Nov/20
![I=∫_0 ^(π/2) (dx/(b^2 tan^2 x+1)) let φ=b tan x ⇒dφ=bsec^2 x dx dx = (φ/(φ^2 +1)) dφ I=∫_0 ^∞ ((φ dφ)/((b^2 +φ^2 )(1+φ^2 ))) = (b/(b^2 −1))∫_0 ^∞ [ (1/(1+φ^2 ))−(1/(b^2 +φ^2 )) ] dφ I= (b/(b^2 −1)) [ tan^(−1) (φ)−tan^(−1) ((φ/b)) ]_0 ^∞ I= (b/(b^2 −1)) [ (π/2) − (π/(2b)) ] I=(π/2) (1−(1/b))((b/(b^2 −1))) = (π/2)(((b−1)/b))((b/((b−1)(b+1)))) I= (π/(2(b+1))) .▲](Q121606.png)
Answered by Olaf last updated on 10/Nov/20
![1) b = 0 I = ∫_0 ^(π/2) dx = (π/2) 2) b = ±1 I = ∫_0 ^(π/2) (dx/(1+tan^2 x)) I = ∫_0 ^(π/2) cos^2 xdx I = ∫_0 ^(π/2) ((1+cos(2x))/2)dx I = [(1/2)x+(1/4)sin(2x)]_0 ^(π/2) I = (π/4) 3) General case : b ≠ 0, b ≠ ±1 u = tanx du = (1+tan^2 x)dx = (1+u^2 )dx I = ∫_0 ^∞ (du/((b^2 u^2 +1)(u^2 +1))) I = (1/(b^2 −1))∫_0 ^∞ [(b^2 /(b^2 u^2 +1))−(1/(1+u^2 ))]du I = (1/(b^2 −1))∫_0 ^∞ [(1/((1/b^2 )+u^2 ))−(1/(1+u^2 ))]du I = (1/(b^2 −1))[barctan(bu)−arctanu]_0 ^∞ I = (1/(b^2 −1))[(b×sign(b)(π/2)−(π/2))−(b(π/4)−(π/4))] I = (1/(b^2 −1))[(π/2)(∣b∣−1)−(π/4)(b−1)] If b>0 : I = (1/(b^2 −1))[(π/2)(b−1)−(π/4)(b−1)] I = (1/(b+1))[(π/2)−(π/4)] = (π/(4(b+1))) If b<0 : I = (1/(b^2 −1))[(π/2)(−b−1)−(π/4)(b−1)] I = (π/(4(b^2 −1)))[2(−b−1)−(b−1)] I = (π/(4(b^2 −1)))(−3b−3) I = −((3π)/(4(b−1)))](Q121607.png)
| ||
Question and Answers Forum | ||
Question Number 121602 by benjo_mathlover last updated on 09/Nov/20 | ||
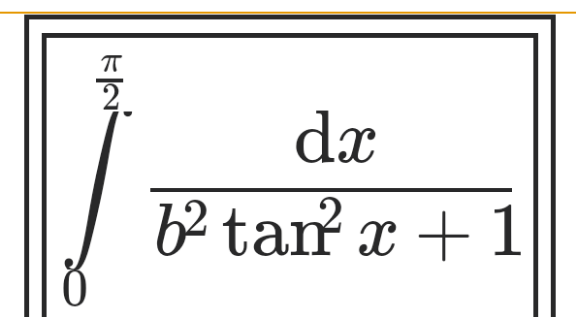 | ||
Answered by liberty last updated on 10/Nov/20 | ||
![I=∫_0 ^(π/2) (dx/(b^2 tan^2 x+1)) let φ=b tan x ⇒dφ=bsec^2 x dx dx = (φ/(φ^2 +1)) dφ I=∫_0 ^∞ ((φ dφ)/((b^2 +φ^2 )(1+φ^2 ))) = (b/(b^2 −1))∫_0 ^∞ [ (1/(1+φ^2 ))−(1/(b^2 +φ^2 )) ] dφ I= (b/(b^2 −1)) [ tan^(−1) (φ)−tan^(−1) ((φ/b)) ]_0 ^∞ I= (b/(b^2 −1)) [ (π/2) − (π/(2b)) ] I=(π/2) (1−(1/b))((b/(b^2 −1))) = (π/2)(((b−1)/b))((b/((b−1)(b+1)))) I= (π/(2(b+1))) .▲](Q121606.png) | ||
| ||
Answered by Olaf last updated on 10/Nov/20 | ||
![1) b = 0 I = ∫_0 ^(π/2) dx = (π/2) 2) b = ±1 I = ∫_0 ^(π/2) (dx/(1+tan^2 x)) I = ∫_0 ^(π/2) cos^2 xdx I = ∫_0 ^(π/2) ((1+cos(2x))/2)dx I = [(1/2)x+(1/4)sin(2x)]_0 ^(π/2) I = (π/4) 3) General case : b ≠ 0, b ≠ ±1 u = tanx du = (1+tan^2 x)dx = (1+u^2 )dx I = ∫_0 ^∞ (du/((b^2 u^2 +1)(u^2 +1))) I = (1/(b^2 −1))∫_0 ^∞ [(b^2 /(b^2 u^2 +1))−(1/(1+u^2 ))]du I = (1/(b^2 −1))∫_0 ^∞ [(1/((1/b^2 )+u^2 ))−(1/(1+u^2 ))]du I = (1/(b^2 −1))[barctan(bu)−arctanu]_0 ^∞ I = (1/(b^2 −1))[(b×sign(b)(π/2)−(π/2))−(b(π/4)−(π/4))] I = (1/(b^2 −1))[(π/2)(∣b∣−1)−(π/4)(b−1)] If b>0 : I = (1/(b^2 −1))[(π/2)(b−1)−(π/4)(b−1)] I = (1/(b+1))[(π/2)−(π/4)] = (π/(4(b+1))) If b<0 : I = (1/(b^2 −1))[(π/2)(−b−1)−(π/4)(b−1)] I = (π/(4(b^2 −1)))[2(−b−1)−(b−1)] I = (π/(4(b^2 −1)))(−3b−3) I = −((3π)/(4(b−1)))](Q121607.png) | ||
| ||