Question Number 121611 by benjo_mathlover last updated on 10/Nov/20
$$\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\mathrm{sin}\:\left(\mathrm{2}\pi\mathrm{x}\right)\mathrm{cos}\:\left(\mathrm{5}\pi\mathrm{x}\right)\:\mathrm{dx}\:?\: \\ $$
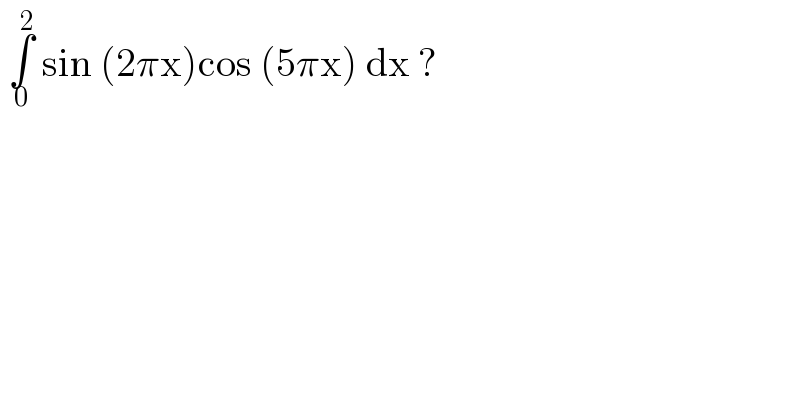
Commented by mr W last updated on 10/Nov/20
![∫_0 ^2 sin (2πx)cos (5πx)dx =(1/2)∫_0 ^2 [sin (7πx)−sin (3πx)]dx =(1/2)[−(1/(7π))cos (7πx)+(1/(3π))cos (3πx)]_0 ^2 =(1/2)[−(1/(7π))(1−1)+(1/(3π))(1−1)] =0](Q121619.png)
$$\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{sin}\:\left(\mathrm{2}\pi{x}\right)\mathrm{cos}\:\left(\mathrm{5}\pi{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \left[\mathrm{sin}\:\left(\mathrm{7}\pi{x}\right)−\mathrm{sin}\:\left(\mathrm{3}\pi{x}\right)\right]{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{7}\pi}\mathrm{cos}\:\left(\mathrm{7}\pi{x}\right)+\frac{\mathrm{1}}{\mathrm{3}\pi}\mathrm{cos}\:\left(\mathrm{3}\pi{x}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{7}\pi}\left(\mathrm{1}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{3}\pi}\left(\mathrm{1}−\mathrm{1}\right)\right] \\ $$$$=\mathrm{0} \\ $$
Commented by MJS_new last updated on 10/Nov/20
$$\mathrm{sin}\:\left(\mathrm{2}\pi\left(\mathrm{2}−{x}\right)\right)=−\mathrm{sin}\:\left(\mathrm{2}\pi{x}\right) \\ $$$$\mathrm{cos}\:\left(\mathrm{5}\pi\left(\mathrm{2}−{x}\right)\right)=\mathrm{cos}\:\left(\mathrm{5}\pi{x}\right) \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}...=\mathrm{0} \\ $$
Answered by MJS_new last updated on 10/Nov/20
$$=\mathrm{0} \\ $$
Commented by benjo_mathlover last updated on 10/Nov/20
$$\mathrm{super}\:\mathrm{fastest}\:\mathrm{prof} \\ $$