... advanced calculus... prove that : Ω =∫_0 ^( ∞) ((sin^4 (x)ln(x))/x^2 )dx=(π/4)(1−γ) γ:euler−mascheroni constant m.n.july.1970


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 121674 by mnjuly1970 last updated on 10/Nov/20

$. . . a d v a n c e d c a l c u l u s . . .$ $p r o v e t h a t :$ $Ω = \int_{0}^{\infty} \frac{{s i n}^{4} (x) l n (x)}{x^{2}} d x = \frac{π}{4} (1 - γ)$ $γ : e u l e r - m a s c h e r o n i c o n s t a n t$ $m . n . j u l y . 1970$
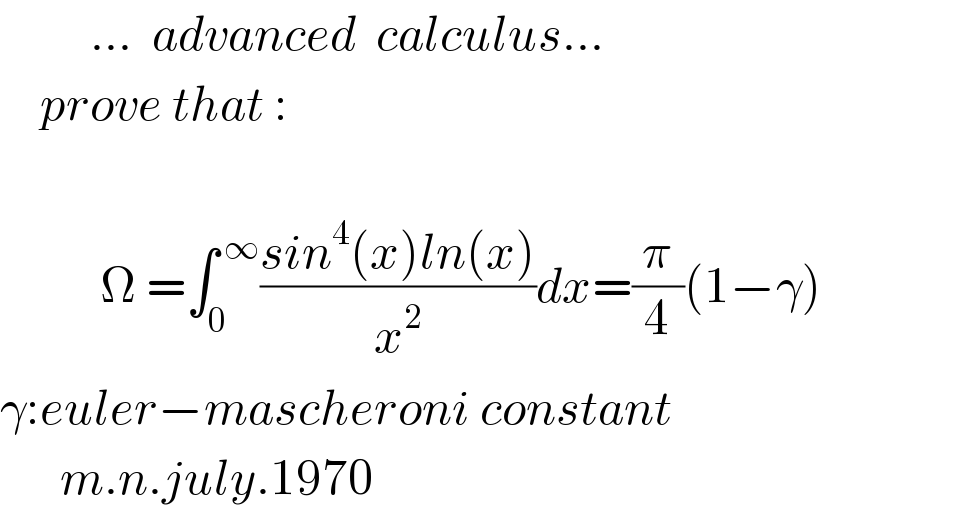
	Answered by mindispower last updated on 11/Nov/20
	$Ω=∫_0 ^∞ ((sin^4 (x))/x^2 )ln(x)dx sin^4 (x)=(1/8)(cos(4x)−4cos(2x)+3) 8Ω=∫_0 ^∞ (cos(4x)−4cos(2x)+3).((ln(x)dx)/x^2 ) by part u=cos(4x)−4cos(2x)+3 dv=((ln(x))/x^2 ),v=−((ln(x))/x)−(1/x) 8Ω=[−(((ln(x)+1))/x)(cos(4x)−4cos(2x)+3)]_0 ^∞ +∫_0 ^∞ (((ln(x)+1))/x)(−4sin(4x)+8sin(2x))dx 8Ω=−4∫_0 ^∞ ((ln(x)+1)/x)(sin(4x)−2sin(2x))dx ⇔−2Ω={∫_0 ^∞ ((ln(x))/x)sin(4x)−2∫((ln(x))/x)sin(2x)}_(=W) +{∫_0 ^∞ ((sin(4x))/x)−2∫_0 ^∞ ((sin(2x))/x)dx}_(=V) a>0,∫_0 ^∞ ((sin(ax))/x)dx=∫_0 ^∞ ((sin(ax))/(ax))d(ax)=(π/2) V=(π/2)−2.(π/2)=−(π/2) ∫_0 ^∞ ((sin(ax))/x)ln(x)=f(a)=(∂/∂t)∫_0 ^∞ sin(ax)x^(t−1) dx∣_(t=0) f(t)=∫_0 ^∞ sin(ax)x^(t−1) dx=Im∫_0 ^∞ e^(iax) x^(t−1) dx iax=−z⇔Im∫_0 ^(i∞) e^(−z) .(((iz)/a))^t .(a/z).(dz/a) =Ima∫_0 ^(i∞) e^(i(π/2)t) ((z/a))^(t−1) e^(−z) dz =Im−(e^(i(π/2)t) /a^t )∫_0 ^∞ z^(t−1) e^(−z) dz =−((sin(((πt)/2))Γ(t))/a^t )=((−sin(((πt)/2))π)/(a^t Γ(1−t)sin(((πt)/2))))=−(π/(2cos((π/2)t)Γ(1−t)a^t )) f′(t)∣_(t=0) =(π/2)(−γ−ln(a)))=−(π/2)(γ+ln(a)) W=f(4)−2f(2)=−(π/2)(γ+ln(4))−2(−(π/2)(γ+ln(2)) =(π/2)γ −2Ω=W+V=(π/2)γ−(π/2)⇒Ω=−((πγ)/4)+(π/4)=(π/4)(1−γ)$
	$Ω = \int_{0}^{\infty} \frac{{s i n}^{4} (x)}{x^{2}} l n (x) d x$ ${s i n}^{4} (x) = \frac{1}{8} (c o s (4 x) - 4 c o s (2 x) + 3)$ $8 Ω = \int_{0}^{\infty} (c o s (4 x) - 4 c o s (2 x) + 3) . \frac{l n (x) d x}{x^{2}}$ $b y p a r t u = c o s (4 x) - 4 c o s (2 x) + 3$ $d v = \frac{l n (x)}{x^{2}}, v = - \frac{l n (x)}{x} - \frac{1}{x}$ $8 Ω = {[- \frac{(l n (x) + 1)}{x} (c o s (4 x) - 4 c o s (2 x) + 3)]}_{0}^{\infty}$ $+ \int_{0}^{\infty} \frac{(l n (x) + 1)}{x} (- 4 s i n (4 x) + 8 s i n (2 x)) d x$ $8 Ω = - 4 \int_{0}^{\infty} \frac{l n (x) + 1}{x} (s i n (4 x) - 2 s i n (2 x)) d x$ $\Leftrightarrow - 2 Ω = {\int_{0}^{\infty} \frac{l n (x)}{x} s i n (4 x) - 2 \int \frac{l n (x)}{x} s i n (2 x)}_{= W}$ $+ {\int_{0}^{\infty} \frac{s i n (4 x)}{x} - 2 \int_{0}^{\infty} \frac{s i n (2 x)}{x} d x}_{= V}$ $a > 0, \int_{0}^{\infty} \frac{s i n (a x)}{x} d x = \int_{0}^{\infty} \frac{s i n (a x)}{a x} d (a x) = \frac{π}{2}$ $V = \frac{π}{2} - 2 . \frac{π}{2} = - \frac{π}{2}$ $\int_{0}^{\infty} \frac{s i n (a x)}{x} l n (x) = f (a) = \frac{\partial}{\partial t} \int_{0}^{\infty} s i n (a x) x^{t - 1} d x ∣_{t = 0}$ $f (t) = \int_{0}^{\infty} s i n (a x) x^{t - 1} d x = I m \int_{0}^{\infty} e^{i a x} x^{t - 1} d x$ $i a x = - z \Leftrightarrow I m \int_{0}^{i \infty} e^{- z} . {(\frac{i z}{a})}^{t} . \frac{a}{z} . \frac{d z}{a}$ $= I m a \int_{0}^{i \infty} e^{i \frac{π}{2} t} {(\frac{z}{a})}^{t - 1} e^{- z} d z$ $= I m - \frac{e^{i \frac{π}{2} t}}{a^{t}} \int_{0}^{\infty} z^{t - 1} e^{- z} d z$ $= - \frac{s i n (\frac{π t}{2}) Γ (t)}{a^{t}} = \frac{- s i n (\frac{π t}{2}) π}{a^{t} Γ (1 - t) s i n (\frac{π t}{2})} = - \frac{π}{2 c o s (\frac{π}{2} t) Γ (1 - t) a^{t}}$ $f^{'} (t) ∣_{t = 0} = \frac{π}{2} (- γ - l n (a))) = - \frac{π}{2} (γ + l n (a))$ $W = f (4) - 2 f (2) = - \frac{π}{2} (γ + l n (4)) - 2 (- \frac{π}{2} (γ + l n (2))$ $= \frac{π}{2} γ$ $- 2 Ω = W + V = \frac{π}{2} γ - \frac{π}{2} \Rightarrow Ω = - \frac{π γ}{4} + \frac{π}{4} = \frac{π}{4} (1 - γ)$
	Commented by mnjuly1970 last updated on 11/Nov/20

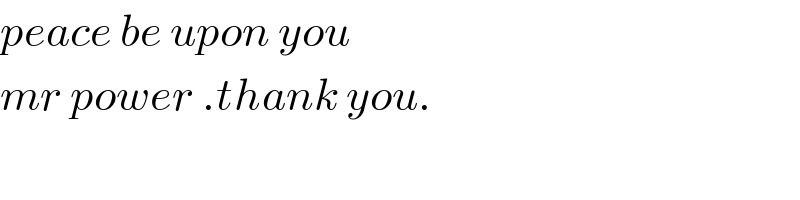
	$p e a c e b e u p o n y o u$ $m r p o w e r . t h a n k y o u .$
	Commented by mindispower last updated on 11/Nov/20

	$w i t h e p l e a s u r s i r$
	Answered by mnjuly1970 last updated on 11/Nov/20

	Answered by mnjuly1970 last updated on 11/Nov/20

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum