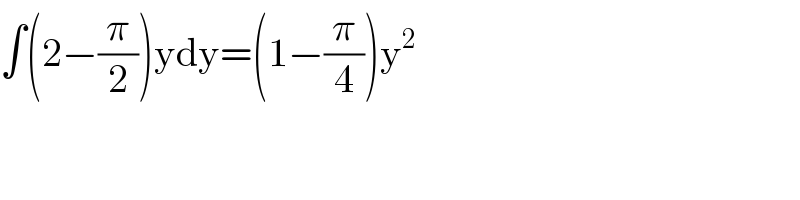Question and Answers Forum
Question Number 121712 by rs4089 last updated on 11/Nov/20
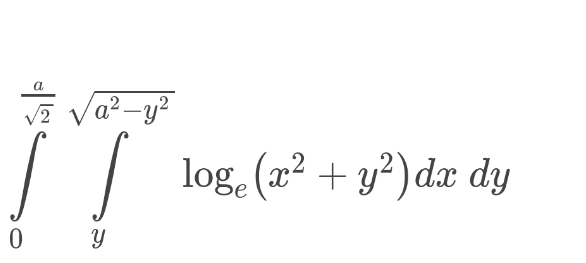
Answered by Ar Brandon last updated on 11/Nov/20
![∫_0 ^(a/( (√2))) ∫_y ^(√(a^2 −y^2 )) ln(x^2 +y^2 )dxdy Let I=∫_y ^(√(a^2 −y^2 )) ln(x^2 +y^2 )dx ⇒I={xln(x^2 +y^2 )−2∫(x^2 /(x^2 +y^2 ))dx}_y ^(√(a^2 −y^2 )) ={xln(x^2 +y^2 )−2∫[1−(y^2 /(x^2 +y^2 ))]dx}_y ^(√(a^2 −y^2 )) =(√(a^2 −y^2 ))ln(a^2 )−yln(2y^2 )−2[x−Arctan((x/y))]_y ^(√(a^2 −y^2 )) =(√(a^2 −y^2 ))ln(a^2 )−yln(2y^2 −2[(√(a^2 −y^2 ))−yArctan(((√(a^2 −y^2 ))/y))−y+yArctan(1)] =(lna^2 −2)(√(a^2 −y^2 ))−yln(2y^2 )+2yArctan(((√(a^2 −y^2 ))/y))+2y−(π/2)y ∫_0 ^(a/( (√2))) (I)dy={(lna^2 −2)∫(√(a^2 −y^2 ))dy−∫yln(2y^2 )dy+2∫yArctan(((√(a^2 −y^2 ))/y))dy+∫(2−(π/2))ydy}_0 ^(a/( (√2)))](Q121755.png)
Commented by Ar Brandon last updated on 11/Nov/20
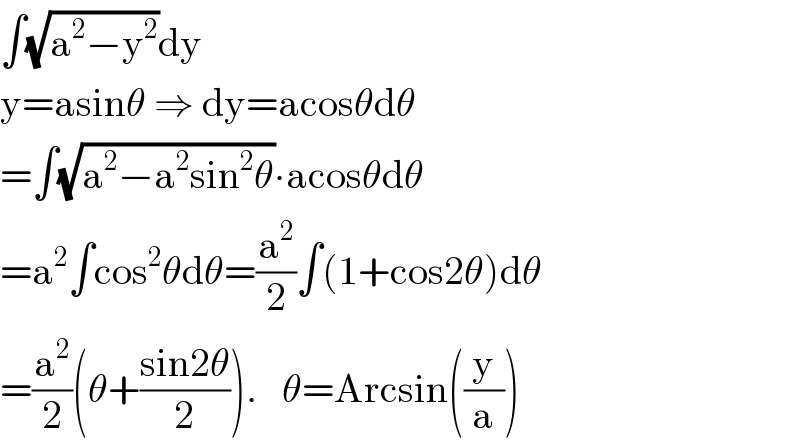
Commented by Ar Brandon last updated on 11/Nov/20
![∫yln(2y^2 )dy=(1/4)∫4yln(2y^2 )dy =((2y^2 [ln(2y^2 )−1])/4)](Q121758.png)
Commented by Ar Brandon last updated on 11/Nov/20
![∫yArctan(((√(a^2 −y^2 ))/y))dy u(y)=Arctan(((√(a^2 −y^2 ))/y)) u′(y)=((y×(−2y)×(1/2)∙(1/( (√(a^2 −y^2 ))))−(√(a^2 −y^2 )))/y^2 ) =−(1/( (√(a^2 −y^2 ))))−((√(a^2 −y^2 ))/y^2 ) v′(y)=y ⇒ v(y)=(y^2 /2) ∫yArctan(((√(a^2 −y^2 ))/y))dy =(y^2 /2)Arctan(((√(a^2 −y^2 ))/y))+(1/2)∫[(y^2 /( (√(a^2 −y^2 ))))+(√(a^2 −y^2 ))] ∫(y^2 /( (√(a^2 −y^2 ))))dy=∫{(a^2 /( (√(a^2 −y^2 ))))−(√(a^2 −y^2 ))}dy ∫(a^2 /( (√(a^2 −y^2 ))))dy=a^2 Arcsin((y/a))](Q121760.png)
Commented by Ar Brandon last updated on 11/Nov/20