
Question and Answers Forum
Question Number 121754 by bemath last updated on 11/Nov/20
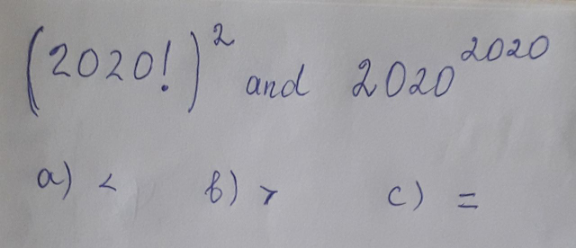
Answered by liberty last updated on 11/Nov/20

Commented by MJS_new last updated on 11/Nov/20
![(1!)^2 =1 ^ 1^1 =1 (2!)^2 =4 2^2 =4 (3!)^2 =36 3^3 =27 (4!)^2 =576 ^ 4^4 =256 ... (n!)^2 ≥n^n ∀n∈N^★ using Stirling′s Approximation lim_(n→∞) (n!− (n^n /e^n )(√(2πn))) =0 and n!>(n^n /e^n )(√(2πn)) (n!)^2 <>n^n (n^(2n) /e^(2n) )2πn<>n^n n^(2n) 2πn<>n^n e^(2n) both sides >0 2nln n +ln n +ln 2π <> nln n +2n (n+1)ln n <> 2n−ln 2π ln n <> 2−((2+ln 2π)/(n+1)) obviously ln n > 2 ∀ n>e^2 [ln n = 2−((2+ln 2π)/(n+1)) ⇒ n≈2.34940] 2020>e^2 ⇒ (2020!)^2 >((2020^(4040) )/e^(4040) )4040π>2020^(2020)](Q121770.png)
Answered by TANMAY PANACEA last updated on 11/Nov/20

| ||
Question and Answers Forum | ||
Question Number 121754 by bemath last updated on 11/Nov/20 | ||
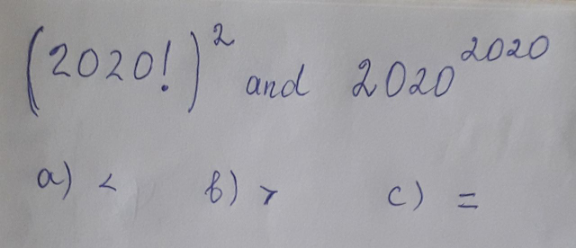 | ||
Answered by liberty last updated on 11/Nov/20 | ||
 | ||
| ||
Commented by MJS_new last updated on 11/Nov/20 | ||
![(1!)^2 =1 ^ 1^1 =1 (2!)^2 =4 2^2 =4 (3!)^2 =36 3^3 =27 (4!)^2 =576 ^ 4^4 =256 ... (n!)^2 ≥n^n ∀n∈N^★ using Stirling′s Approximation lim_(n→∞) (n!− (n^n /e^n )(√(2πn))) =0 and n!>(n^n /e^n )(√(2πn)) (n!)^2 <>n^n (n^(2n) /e^(2n) )2πn<>n^n n^(2n) 2πn<>n^n e^(2n) both sides >0 2nln n +ln n +ln 2π <> nln n +2n (n+1)ln n <> 2n−ln 2π ln n <> 2−((2+ln 2π)/(n+1)) obviously ln n > 2 ∀ n>e^2 [ln n = 2−((2+ln 2π)/(n+1)) ⇒ n≈2.34940] 2020>e^2 ⇒ (2020!)^2 >((2020^(4040) )/e^(4040) )4040π>2020^(2020)](Q121770.png) | ||
Answered by TANMAY PANACEA last updated on 11/Nov/20 | ||
 | ||
| ||