Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 121832 by bemath last updated on 12/Nov/20

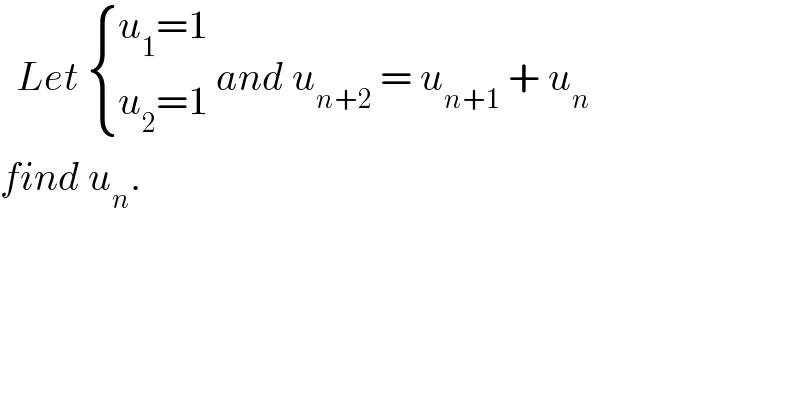
Let { ((u_1 =1)),((u_2 =1)) :} and u_(n+2) = u_(n+1) + u_n find u_n .

$$\:\:{Let}\:\begin{cases}{{u}_{\mathrm{1}} =\mathrm{1}}\\{{u}_{\mathrm{2}} =\mathrm{1}}\end{cases}\:{and}\:{u}_{{n}+\mathrm{2}} \:=\:{u}_{{n}+\mathrm{1}} \:+\:{u}_{{n}} \\ $$$${find}\:{u}_{{n}} . \\ $$

Commented by bemath last updated on 12/Nov/20

thank you both

$${thank}\:{you}\:{both} \\ $$

Answered by mr W last updated on 12/Nov/20

q^2 −q−1=0 q=((1±(√5))/2) u_n =A(((1+(√5))/2))^n +B(((1−(√5))/2))^n u_0 =A+B=u_2 −u_1 =1−1=0 ⇒A=−B u_1 =A(((1+(√5))/2))+B(((1−(√5))/2))=1 A[((1+(√5))/2)−((1−(√5))/2)]=1 ⇒A=(1/( (√5))) ⇒B=−(1/( (√5))) ⇒u_n =(1/( (√5)))[(((1+(√5))/2))^n −(((1−(√5))/2))^n ]

$${q}^{\mathrm{2}} −{q}−\mathrm{1}=\mathrm{0} \\ $$$${q}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${u}_{{n}} ={A}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} +{B}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \\ $$$${u}_{\mathrm{0}} ={A}+{B}={u}_{\mathrm{2}} −{u}_{\mathrm{1}} =\mathrm{1}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{A}=−{B} \\ $$$${u}_{\mathrm{1}} ={A}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)+{B}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\mathrm{1} \\ $$$${A}\left[\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right]=\mathrm{1} \\ $$$$\Rightarrow{A}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow{B}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \right] \\ $$

Answered by Dwaipayan Shikari last updated on 12/Nov/20

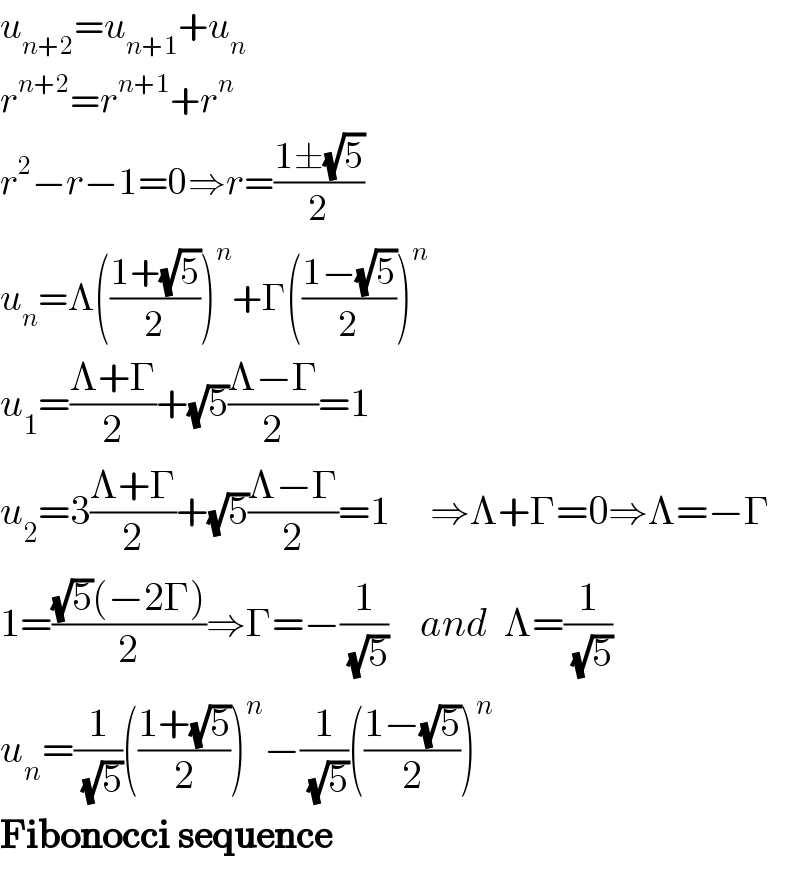
u_(n+2) =u_(n+1) +u_n r^(n+2) =r^(n+1) +r^n r^2 −r−1=0⇒r=((1±(√5))/2) u_n =Λ(((1+(√5))/2))^n +Γ(((1−(√5))/2))^n u_1 =((Λ+Γ)/2)+(√5)((Λ−Γ)/2)=1 u_2 =3((Λ+Γ)/2)+(√5)((Λ−Γ)/2)=1 ⇒Λ+Γ=0⇒Λ=−Γ 1=(((√5)(−2Γ))/2)⇒Γ=−(1/( (√5))) and Λ=(1/( (√5))) u_n =(1/( (√5)))(((1+(√5))/2))^n −(1/( (√5)))(((1−(√5))/2))^n Fibonocci sequence

$${u}_{{n}+\mathrm{2}} ={u}_{{n}+\mathrm{1}} +{u}_{{n}} \\ $$$${r}^{{n}+\mathrm{2}} ={r}^{{n}+\mathrm{1}} +{r}^{{n}} \\ $$$${r}^{\mathrm{2}} −{r}−\mathrm{1}=\mathrm{0}\Rightarrow{r}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${u}_{{n}} =\Lambda\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} +\Gamma\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \\ $$$${u}_{\mathrm{1}} =\frac{\Lambda+\Gamma}{\mathrm{2}}+\sqrt{\mathrm{5}}\frac{\Lambda−\Gamma}{\mathrm{2}}=\mathrm{1} \\ $$$${u}_{\mathrm{2}} =\mathrm{3}\frac{\Lambda+\Gamma}{\mathrm{2}}+\sqrt{\mathrm{5}}\frac{\Lambda−\Gamma}{\mathrm{2}}=\mathrm{1}\:\:\:\:\:\Rightarrow\Lambda+\Gamma=\mathrm{0}\Rightarrow\Lambda=−\Gamma \\ $$$$\mathrm{1}=\frac{\sqrt{\mathrm{5}}\left(−\mathrm{2}\Gamma\right)}{\mathrm{2}}\Rightarrow\Gamma=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\:\:\:{and}\:\:\Lambda=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${u}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} −\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \\ $$$$\boldsymbol{\mathrm{Fibonocci}}\:\boldsymbol{\mathrm{sequence}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com