
Question and Answers Forum
Question Number 121859 by Bird last updated on 12/Nov/20
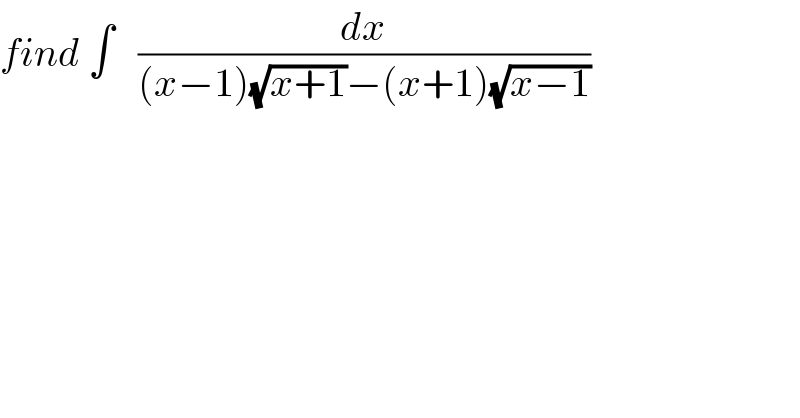
Answered by ajfour last updated on 12/Nov/20
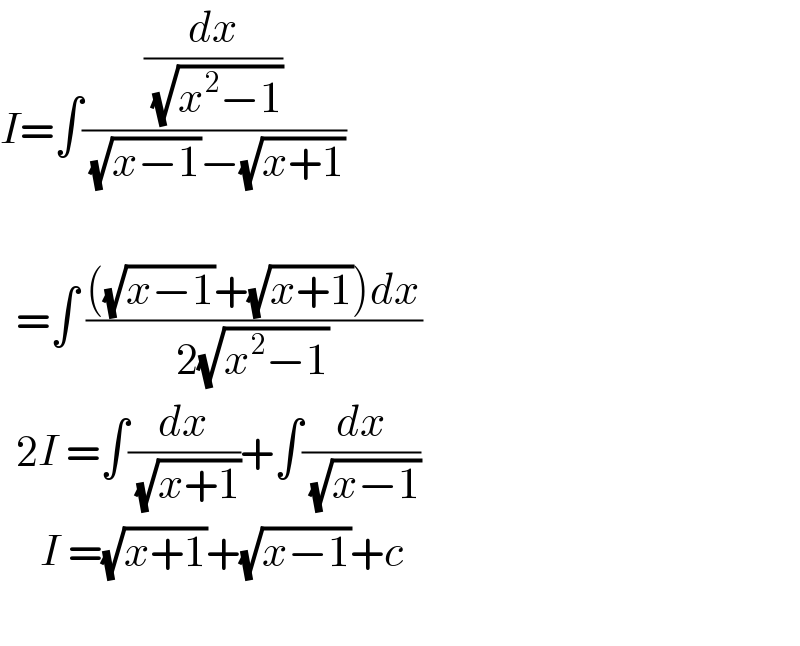
Answered by liberty last updated on 12/Nov/20
![(1/((x−1)(√(x+1)) −(x+1)(√(x−1)))) . (((x−1)(√(x+1))+(x+1)(√(x−1)))/((x−1)(√(x+1))+(x+1)(√(x−1)))) = (((x−1)(√(x+1))+(x+1)(√(x−1)))/((x−1)^2 (x+1)+(x^2 −1)(√(x^2 −1))−(x^2 −1)(√(x^2 −1))−(x+1)^2 (x−1))) = (((x−1)(√(x+1))+(x+1)(√(x−1)))/((x−1)^2 (x+1)−(x+1)^2 (x−1))) = (((x−1)(√(x+1))+(x+1)(√(x−1)))/((x^2 −1){x−1−x−1})) = (((x−1)(√(x+1))+(x+1)(√(x−1)))/(−2(x^2 −1))) = −(1/2) [ ((√(x+1))/(x+1)) +((√(x−1))/(x−1)) ] = −(1/2) [ (1/( (√(x+1))))+(1/( (√(x−1)))) ] then I = −(1/2)∫ [ (x+1)^(−(1/2)) +(x−1)^(−(1/2)) ] dx I = −(1/2) [ 2(√(x+1)) +2(√(x−1)) ] + c I = −(√(x+1)) −(√(x−1)) + c. ▲](Q121874.png)
| ||
Question and Answers Forum | ||
Question Number 121859 by Bird last updated on 12/Nov/20 | ||
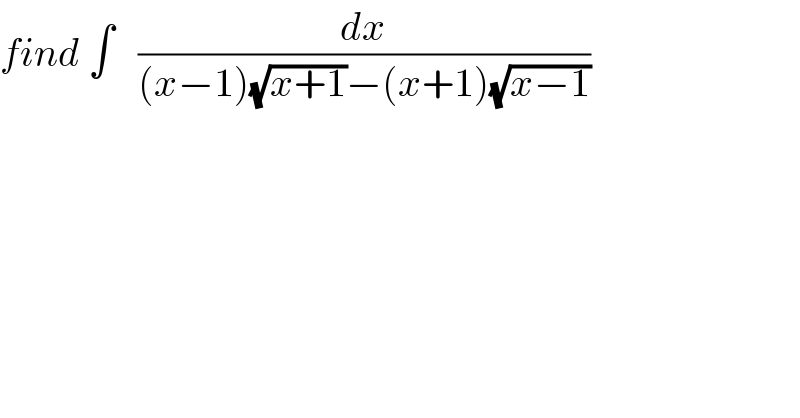 | ||
Answered by ajfour last updated on 12/Nov/20 | ||
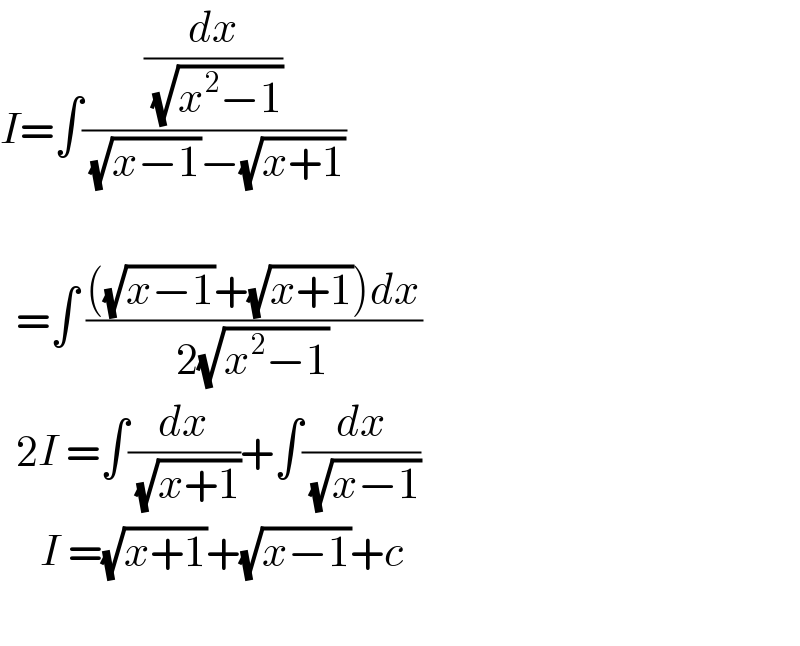 | ||
| ||
Answered by liberty last updated on 12/Nov/20 | ||
![(1/((x−1)(√(x+1)) −(x+1)(√(x−1)))) . (((x−1)(√(x+1))+(x+1)(√(x−1)))/((x−1)(√(x+1))+(x+1)(√(x−1)))) = (((x−1)(√(x+1))+(x+1)(√(x−1)))/((x−1)^2 (x+1)+(x^2 −1)(√(x^2 −1))−(x^2 −1)(√(x^2 −1))−(x+1)^2 (x−1))) = (((x−1)(√(x+1))+(x+1)(√(x−1)))/((x−1)^2 (x+1)−(x+1)^2 (x−1))) = (((x−1)(√(x+1))+(x+1)(√(x−1)))/((x^2 −1){x−1−x−1})) = (((x−1)(√(x+1))+(x+1)(√(x−1)))/(−2(x^2 −1))) = −(1/2) [ ((√(x+1))/(x+1)) +((√(x−1))/(x−1)) ] = −(1/2) [ (1/( (√(x+1))))+(1/( (√(x−1)))) ] then I = −(1/2)∫ [ (x+1)^(−(1/2)) +(x−1)^(−(1/2)) ] dx I = −(1/2) [ 2(√(x+1)) +2(√(x−1)) ] + c I = −(√(x+1)) −(√(x−1)) + c. ▲](Q121874.png) | ||
| ||