
Question and Answers Forum
Question Number 121890 by oustmuchiya@gmail.com last updated on 12/Nov/20

Commented by liberty last updated on 12/Nov/20
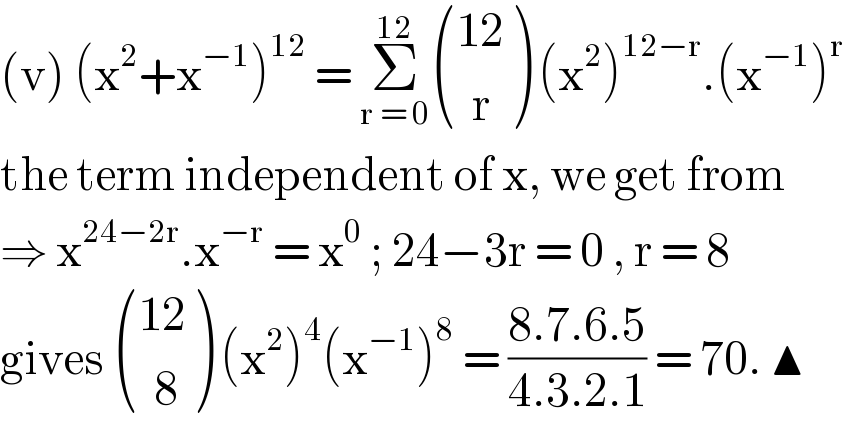
Answered by bemath last updated on 12/Nov/20
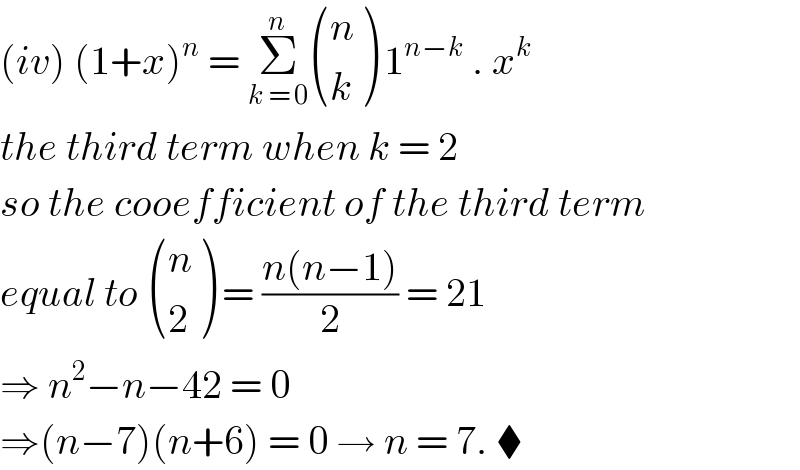
Answered by TANMAY PANACEA last updated on 12/Nov/20
![i)(1−(x/2))^5 =1−5C_1 ((x/2))+5C_2 ((x/2))^2 −5C_3 ((x/2))^3 +5C_4 ((x/2))^4 −((x/2))^5 ii)(1+(x/2))^5 +(1−(x/2))^5 ⇚note odd terms cancelled =2[1+5C_2 ((x/2))^2 +5C_4 ((x/2))^4 ] iii)put x=0.1to find (1.05)^5 +(0.95)^4](Q121912.png)
| ||
Question and Answers Forum | ||
Question Number 121890 by oustmuchiya@gmail.com last updated on 12/Nov/20 | ||
 | ||
Commented by liberty last updated on 12/Nov/20 | ||
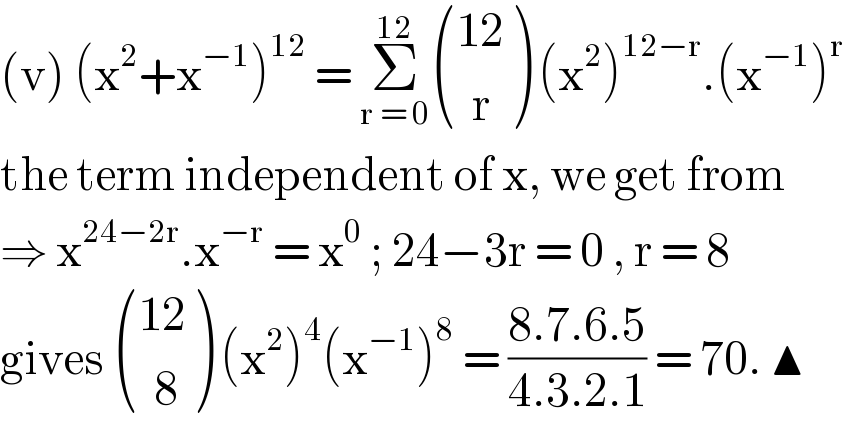 | ||
Answered by bemath last updated on 12/Nov/20 | ||
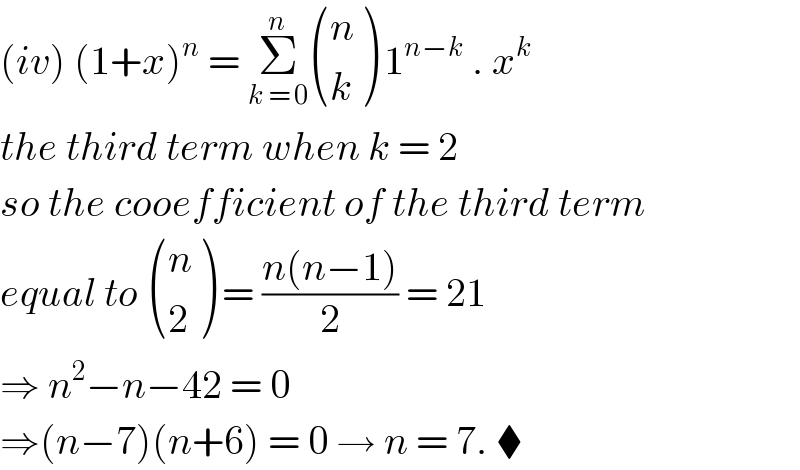 | ||
| ||
Answered by TANMAY PANACEA last updated on 12/Nov/20 | ||
![i)(1−(x/2))^5 =1−5C_1 ((x/2))+5C_2 ((x/2))^2 −5C_3 ((x/2))^3 +5C_4 ((x/2))^4 −((x/2))^5 ii)(1+(x/2))^5 +(1−(x/2))^5 ⇚note odd terms cancelled =2[1+5C_2 ((x/2))^2 +5C_4 ((x/2))^4 ] iii)put x=0.1to find (1.05)^5 +(0.95)^4](Q121912.png) | ||
| ||