Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 121918 by greg_ed last updated on 12/Nov/20

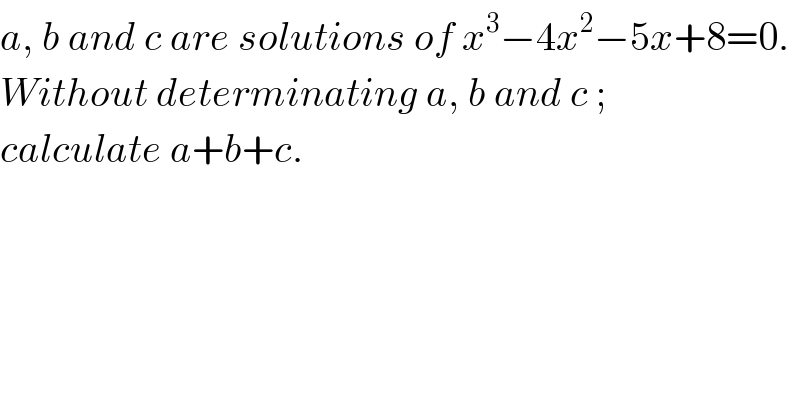
a, b and c are solutions of x^3 −4x^2 −5x+8=0. Without determinating a, b and c ; calculate a+b+c.

$${a},\:{b}\:{and}\:{c}\:{are}\:{solutions}\:{of}\:{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{8}=\mathrm{0}. \\ $$$${Without}\:{determinating}\:{a},\:{b}\:{and}\:{c}\:;\: \\ $$$${calculate}\:{a}+{b}+{c}. \\ $$

Commented by mr W last updated on 12/Nov/20

a+b+c=4 ab+bc+ca=−5 abc=−8

$${a}+{b}+{c}=\mathrm{4} \\ $$$${ab}+{bc}+{ca}=−\mathrm{5} \\ $$$${abc}=−\mathrm{8} \\ $$

Commented by greg_ed last updated on 12/Nov/20

please, mr W : it′s not very very clear for me !

$$\mathrm{please},\:\mathrm{mr}\:\mathrm{W}\::\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{very}\:\mathrm{very}\:\mathrm{clear}\:\mathrm{for}\: \\ $$$$\mathrm{me}\:! \\ $$

Commented by physicstutes last updated on 12/Nov/20

Generally if α, β and γ are roots of the equation, ax^3 + bx^2 + cx + d = 0 then α + β + γ = −(b/a) αβγ = −(d/a)

$$\mathrm{Generally}\:\mathrm{if}\:\alpha,\:\beta\:\mathrm{and}\:\gamma\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}, \\ $$$$\:\:\:\:{ax}^{\mathrm{3}} \:+\:{bx}^{\mathrm{2}} \:+\:{cx}\:+\:{d}\:=\:\mathrm{0} \\ $$$$\mathrm{then}\:\alpha\:+\:\beta\:+\:\gamma\:=\:−\frac{{b}}{{a}} \\ $$$$\:\:\:\:\alpha\beta\gamma\:=\:−\frac{{d}}{{a}} \\ $$

Commented by greg_ed last updated on 12/Nov/20

thanks, physicstutes !

$$\boldsymbol{\mathrm{thanks}},\:\boldsymbol{\mathrm{physicstutes}}\:! \\ $$

Commented by MJS_new last updated on 12/Nov/20

(x−a)(x−b)(x−c)=0 x^3 −(a+b+c)x^2 +(ab+ac+bc)x− abc=0 x^3 − 4 x^2 + (−5) x−(−8)=0

$$\left({x}−{a}\right)\left({x}−{b}\right)\left({x}−{c}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\left({a}+{b}+{c}\right){x}^{\mathrm{2}} +\left({ab}+{ac}+{bc}\right){x}−\:{abc}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\:\:\:\:\:\:\:\:\left(−\mathrm{5}\right)\:\:\:\:\:{x}−\left(−\mathrm{8}\right)=\mathrm{0} \\ $$

Commented by greg_ed last updated on 12/Nov/20

ok, MJS_new ! it′s cool !

$$\boldsymbol{\mathrm{ok}},\:\boldsymbol{\mathrm{MJS\_new}}\:!\:\boldsymbol{\mathrm{it}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{cool}}\:! \\ $$

Answered by Dwaipayan Shikari last updated on 12/Nov/20

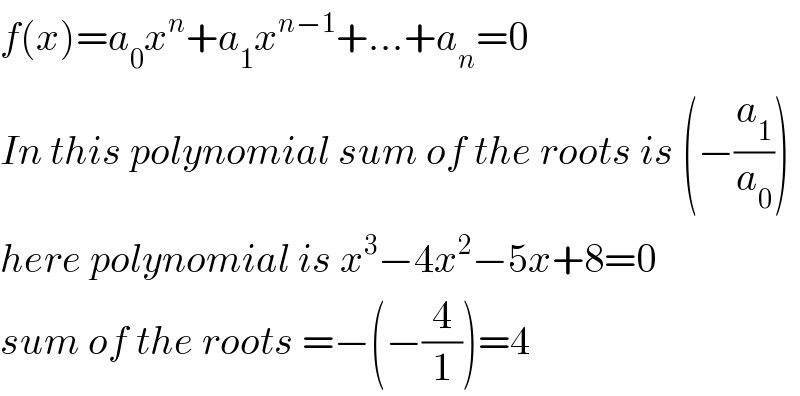
f(x)=a_0 x^n +a_1 x^(n−1) +...+a_n =0 In this polynomial sum of the roots is (−(a_1 /a_0 )) here polynomial is x^3 −4x^2 −5x+8=0 sum of the roots =−(−(4/1))=4

$${f}\left({x}\right)={a}_{\mathrm{0}} {x}^{{n}} +{a}_{\mathrm{1}} {x}^{{n}−\mathrm{1}} +...+{a}_{{n}} =\mathrm{0} \\ $$$${In}\:{this}\:{polynomial}\:{sum}\:{of}\:{the}\:{roots}\:{is}\:\left(−\frac{{a}_{\mathrm{1}} }{{a}_{\mathrm{0}} }\right) \\ $$$${here}\:{polynomial}\:{is}\:{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{8}=\mathrm{0} \\ $$$${sum}\:{of}\:{the}\:{roots}\:=−\left(−\frac{\mathrm{4}}{\mathrm{1}}\right)=\mathrm{4} \\ $$

Commented by greg_ed last updated on 12/Nov/20

thanks, Dwaipayan Shikari !

$$\boldsymbol{\mathrm{thanks}},\:\boldsymbol{\mathrm{Dwaipayan}}\:\boldsymbol{\mathrm{Shikari}}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com