Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 121958 by bemath last updated on 13/Nov/20

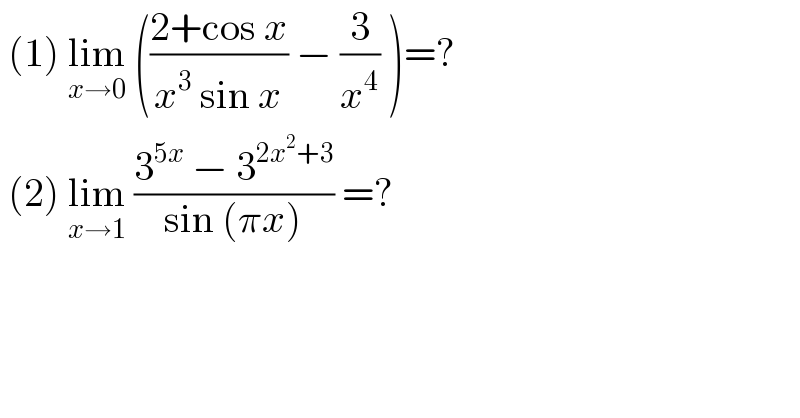
(1) lim_(x→0) (((2+cos x)/(x^3 sin x)) − (3/x^4 ) )=? (2) lim_(x→1) ((3^(5x) − 3^(2x^2 +3) )/(sin (πx))) =?

$$\:\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2}+\mathrm{cos}\:{x}}{{x}^{\mathrm{3}} \:\mathrm{sin}\:{x}}\:−\:\frac{\mathrm{3}}{{x}^{\mathrm{4}} }\:\right)=? \\ $$$$\:\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{3}^{\mathrm{5}{x}} \:−\:\mathrm{3}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}} }{\mathrm{sin}\:\left(\pi{x}\right)}\:=?\: \\ $$

Answered by liberty last updated on 13/Nov/20

(••) lim_(x→1) ((3^(5x) −3^(2x^2 +3) )/(sin πx)) [ letx = 1+η ] lim_(η→0) ((3^(5+5η) −3^(2η^2 +4η+5) )/(−sin πη)) = lim_(η→0) ((3^5 (3^(2η^2 +4η) −3^(5η) ))/(sin πη)) = (3^5 /π)×lim_(η→0) ((ηπ)/(sin ηπ)) ×lim_(η→0) ((3^(2η^2 +4η) −3^(5η) )/η) = ((243)/π) × 1 × lim_(η→0) (((4η+4)ln 3. 3^(2η^2 +4η) −5.ln 3.3^(5η) )/1) = ((243)/π) × (4ln 3−5ln 3)= ((243.ln ((1/3)))/π). ▲

$$\left(\bullet\bullet\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{3}^{\mathrm{5x}} −\mathrm{3}^{\mathrm{2x}^{\mathrm{2}} +\mathrm{3}} }{\mathrm{sin}\:\pi\mathrm{x}}\:\:\:\left[\:\mathrm{letx}\:=\:\mathrm{1}+\eta\:\right]\: \\ $$$$\:\underset{\eta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}^{\mathrm{5}+\mathrm{5}\eta} −\mathrm{3}^{\mathrm{2}\eta^{\mathrm{2}} +\mathrm{4}\eta+\mathrm{5}} }{−\mathrm{sin}\:\pi\eta}\:=\:\underset{\eta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}^{\mathrm{5}} \left(\mathrm{3}^{\mathrm{2}\eta^{\mathrm{2}} +\mathrm{4}\eta} −\mathrm{3}^{\mathrm{5}\eta} \right)}{\mathrm{sin}\:\pi\eta} \\ $$$$=\:\frac{\mathrm{3}^{\mathrm{5}} }{\pi}×\underset{\eta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\eta\pi}{\mathrm{sin}\:\eta\pi}\:×\underset{\eta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}^{\mathrm{2}\eta^{\mathrm{2}} +\mathrm{4}\eta} −\mathrm{3}^{\mathrm{5}\eta} }{\eta} \\ $$$$=\:\frac{\mathrm{243}}{\pi}\:×\:\mathrm{1}\:×\:\underset{\eta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{4}\eta+\mathrm{4}\right)\mathrm{ln}\:\mathrm{3}.\:\mathrm{3}^{\mathrm{2}\eta^{\mathrm{2}} +\mathrm{4}\eta} −\mathrm{5}.\mathrm{ln}\:\mathrm{3}.\mathrm{3}^{\mathrm{5}\eta} }{\mathrm{1}} \\ $$$$=\:\frac{\mathrm{243}}{\pi}\:×\:\left(\mathrm{4ln}\:\mathrm{3}−\mathrm{5ln}\:\mathrm{3}\right)=\:\frac{\mathrm{243}.\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\pi}.\:\blacktriangle \\ $$

Answered by Dwaipayan Shikari last updated on 13/Nov/20

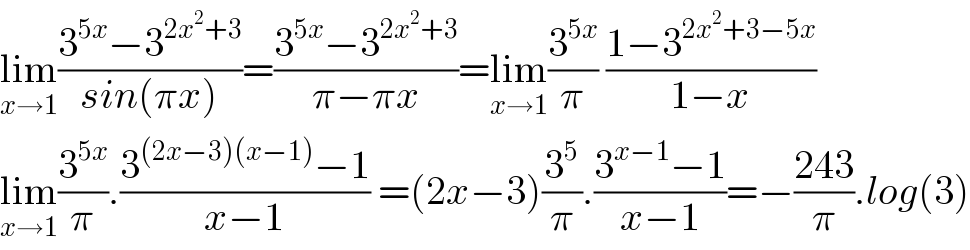
lim_(x→1) ((3^(5x) −3^(2x^2 +3) )/(sin(πx)))=((3^(5x) −3^(2x^2 +3) )/(π−πx))=lim_(x→1) (3^(5x) /π) ((1−3^(2x^2 +3−5x) )/(1−x)) lim_(x→1) (3^(5x) /π).((3^((2x−3)(x−1)) −1)/(x−1)) =(2x−3)(3^5 /π).((3^(x−1) −1)/(x−1))=−((243)/π).log(3)

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{3}^{\mathrm{5}{x}} −\mathrm{3}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}} }{{sin}\left(\pi{x}\right)}=\frac{\mathrm{3}^{\mathrm{5}{x}} −\mathrm{3}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}} }{\pi−\pi{x}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{3}^{\mathrm{5}{x}} }{\pi}\:\frac{\mathrm{1}−\mathrm{3}^{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}−\mathrm{5}{x}} }{\mathrm{1}−{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{3}^{\mathrm{5}{x}} }{\pi}.\frac{\mathrm{3}^{\left(\mathrm{2}{x}−\mathrm{3}\right)\left({x}−\mathrm{1}\right)} −\mathrm{1}}{{x}−\mathrm{1}}\:=\left(\mathrm{2}{x}−\mathrm{3}\right)\frac{\mathrm{3}^{\mathrm{5}} }{\pi}.\frac{\mathrm{3}^{{x}−\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}=−\frac{\mathrm{243}}{\pi}.{log}\left(\mathrm{3}\right) \\ $$

Answered by liberty last updated on 13/Nov/20

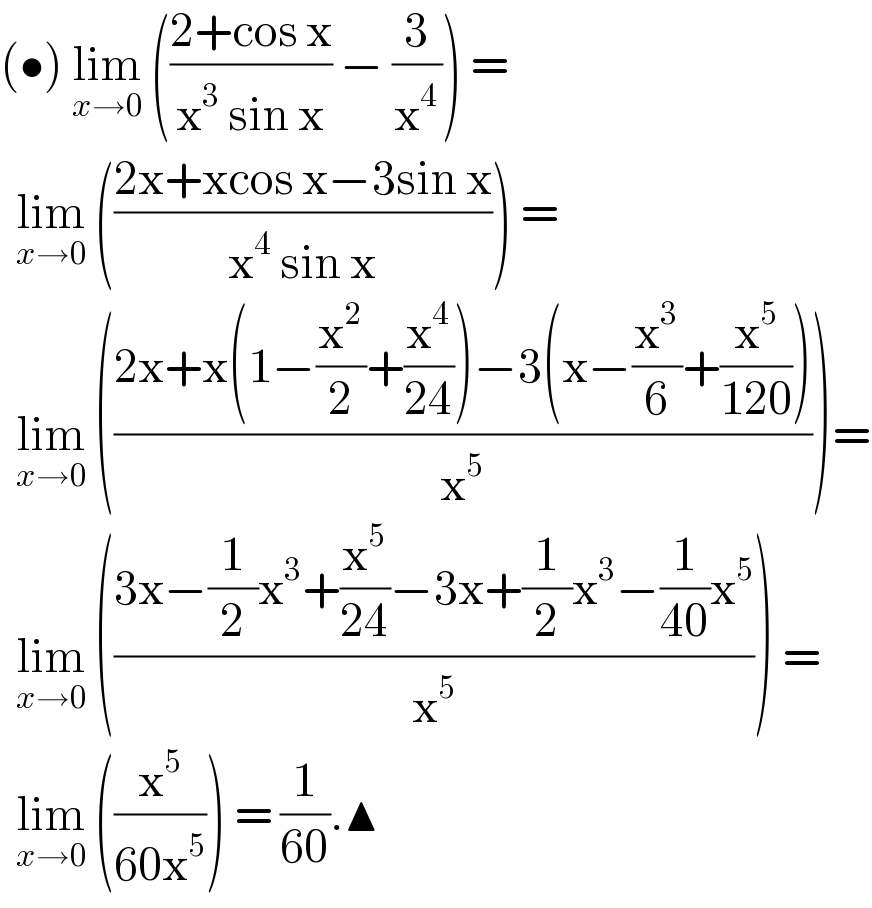
(•) lim_(x→0) (((2+cos x)/(x^3 sin x)) − (3/x^4 )) = lim_(x→0) (((2x+xcos x−3sin x)/(x^4 sin x))) = lim_(x→0) (((2x+x(1−(x^2 /2)+(x^4 /(24)))−3(x−(x^3 /6)+(x^5 /(120))))/x^5 ))= lim_(x→0) (((3x−(1/2)x^3 +(x^5 /(24))−3x+(1/2)x^3 −(1/(40))x^5 )/x^5 )) = lim_(x→0) ((x^5 /(60x^5 ))) = (1/(60)).▲

$$\left(\bullet\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2}+\mathrm{cos}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} \:\mathrm{sin}\:\mathrm{x}}\:−\:\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{4}} }\right)\:=\: \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2x}+\mathrm{xcos}\:\mathrm{x}−\mathrm{3sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{4}} \:\mathrm{sin}\:\mathrm{x}}\right)\:= \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2x}+\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{24}}\right)−\mathrm{3}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{120}}\right)}{\mathrm{x}^{\mathrm{5}} }\right)= \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{3x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{24}}−\mathrm{3x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{40}}\mathrm{x}^{\mathrm{5}} }{\mathrm{x}^{\mathrm{5}} }\right)\:= \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{60x}^{\mathrm{5}} }\right)\:=\:\frac{\mathrm{1}}{\mathrm{60}}.\blacktriangle\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com