Question and Answers Forum
Question Number 121962 by bemath last updated on 13/Nov/20
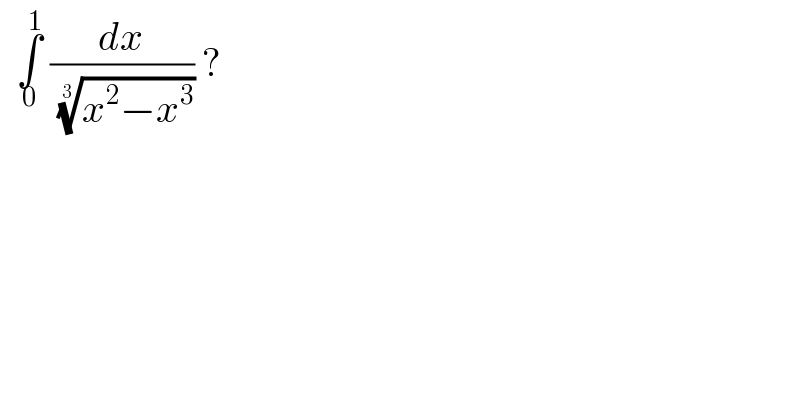
Answered by MJS_new last updated on 13/Nov/20
![∫_0 ^1 (dx/((x^2 −x^3 )^(1/3) ))=∫_0 ^1 (dx/(x^(2/3) (1−x)^(1/3) ))= [t=(x^(1/3) /((1−x)^(1/3) )) → dx=3x^(2/3) (1−x)^(4/3) dt] =3∫_0 ^∞ (dt/(t^3 +1))=∫_0 ^∞ (dt/(t+1))−(1/2)∫_0 ^∞ ((2t−1)/(t^2 −t+1))+(3/2)∫_0 ^∞ (dt/(t^2 −t+1))= =[ln ∣t+1∣ −(1/2)ln (t^2 −t+1) +(√3)arctan ((2t−1)/( (√3)))]_0 ^∞ = =((2π(√3))/3)](Q121968.png)
Commented by bemath last updated on 13/Nov/20

Commented by MJS_new last updated on 13/Nov/20

Commented by MJS_new last updated on 13/Nov/20
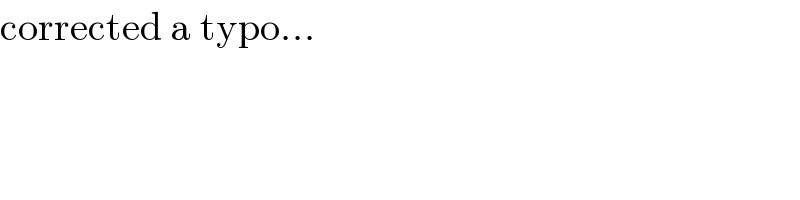
Commented by bemath last updated on 13/Nov/20
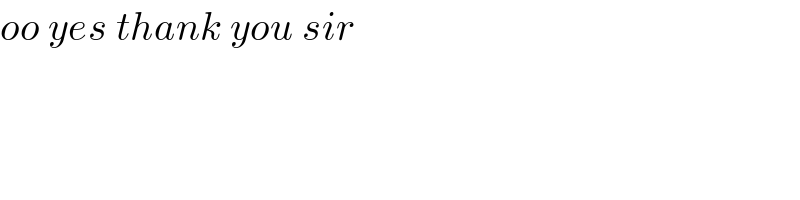
Answered by Dwaipayan Shikari last updated on 13/Nov/20