
Question and Answers Forum
Question Number 122002 by liberty last updated on 13/Nov/20
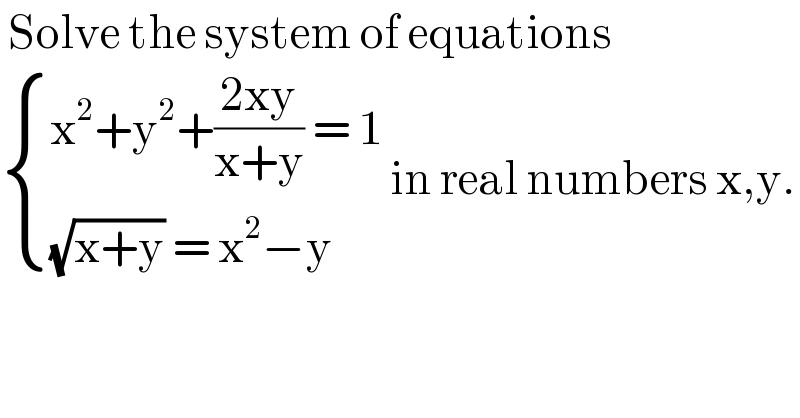
Answered by MJS_new last updated on 13/Nov/20
![(√(x+y))=x^2 −y squaring & transforming y^2 −(2x^2 +1)y+(x^4 −x)=0 ⇒ (a) y=x^2 −x∨(b) y=x^2 +x+1 [we have some limitations but let′s just go on and see what will happen] inserting in (1) we get (a) x^6 −2x^5 +2x^4 +2x^3 −3x^2 =0 (b) x^6 +4x^5 +9x^4 +14x^3 +10x^2 +4x=0 ⇒ (a) x^2 (x−1)(x+1)(x^2 −2x+3)=0 (b) x(x+2)(x^4 +2x^3 +5x^2 +4x+2)=0 ⇒ (a) x=−1∨x=0∨x=1 ⇒ y=2 ^ ^ ∨y=0∨y=0 (b) x=−2∨x=0 ⇒ y=3 ∨y=1 testing all pairs we get (x∣y)=(1∣0)∨(−2∣3)](Q122011.png)
Commented by liberty last updated on 13/Nov/20

Answered by liberty last updated on 13/Nov/20

| ||
Question and Answers Forum | ||
Question Number 122002 by liberty last updated on 13/Nov/20 | ||
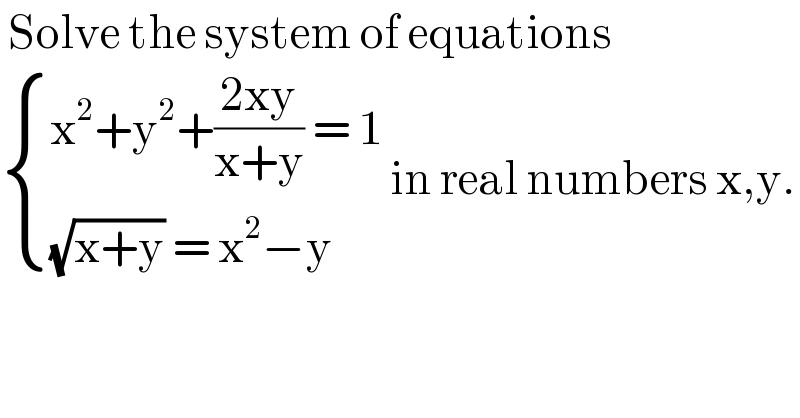 | ||
Answered by MJS_new last updated on 13/Nov/20 | ||
![(√(x+y))=x^2 −y squaring & transforming y^2 −(2x^2 +1)y+(x^4 −x)=0 ⇒ (a) y=x^2 −x∨(b) y=x^2 +x+1 [we have some limitations but let′s just go on and see what will happen] inserting in (1) we get (a) x^6 −2x^5 +2x^4 +2x^3 −3x^2 =0 (b) x^6 +4x^5 +9x^4 +14x^3 +10x^2 +4x=0 ⇒ (a) x^2 (x−1)(x+1)(x^2 −2x+3)=0 (b) x(x+2)(x^4 +2x^3 +5x^2 +4x+2)=0 ⇒ (a) x=−1∨x=0∨x=1 ⇒ y=2 ^ ^ ∨y=0∨y=0 (b) x=−2∨x=0 ⇒ y=3 ∨y=1 testing all pairs we get (x∣y)=(1∣0)∨(−2∣3)](Q122011.png) | ||
| ||
Commented by liberty last updated on 13/Nov/20 | ||
 | ||
Answered by liberty last updated on 13/Nov/20 | ||
 | ||
| ||