Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 122007 by ZiYangLee last updated on 13/Nov/20

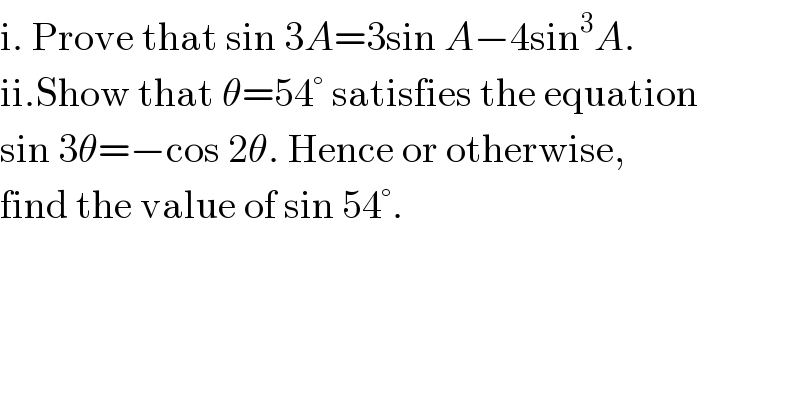
i. Prove that sin 3A=3sin A−4sin^3 A. ii.Show that θ=54° satisfies the equation sin 3θ=−cos 2θ. Hence or otherwise, find the value of sin 54°.

$$\mathrm{i}.\:\mathrm{Prove}\:\mathrm{that}\:\mathrm{sin}\:\mathrm{3}{A}=\mathrm{3sin}\:{A}−\mathrm{4sin}^{\mathrm{3}} {A}. \\ $$$$\mathrm{ii}.\mathrm{Show}\:\mathrm{that}\:\theta=\mathrm{54}°\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{sin}\:\mathrm{3}\theta=−\mathrm{cos}\:\mathrm{2}\theta.\:\mathrm{Hence}\:\mathrm{or}\:\mathrm{otherwise},\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}\:\mathrm{54}°. \\ $$

Answered by TANMAY PANACEA last updated on 13/Nov/20

sin(3A)=sin2AcosA+cos2AsinA =2sinA(1−sin^2 A)+(1−2sin^2 A)sinA =2s−2s^3 +s−2s^3 =3s−4s^3 [s=sinA]

$${sin}\left(\mathrm{3}{A}\right)={sin}\mathrm{2}{AcosA}+{cos}\mathrm{2}{AsinA} \\ $$$$=\mathrm{2}{sinA}\left(\mathrm{1}−{sin}^{\mathrm{2}} {A}\right)+\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {A}\right){sinA} \\ $$$$=\mathrm{2}{s}−\mathrm{2}{s}^{\mathrm{3}} +{s}−\mathrm{2}{s}^{\mathrm{3}} =\mathrm{3}{s}−\mathrm{4}{s}^{\mathrm{3}} \:\:\left[{s}={sinA}\right] \\ $$

Answered by TANMAY PANACEA last updated on 13/Nov/20

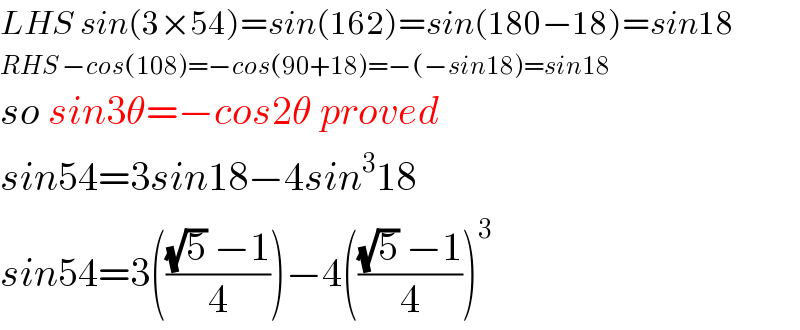
LHS sin(3×54)=sin(162)=sin(180−18)=sin18 RHS −cos(108)=−cos(90+18)=−(−sin18)=sin18 so sin3θ=−cos2θ proved sin54=3sin18−4sin^3 18 sin54=3((((√5) −1)/4))−4((((√5) −1)/4))^3

$${LHS}\:{sin}\left(\mathrm{3}×\mathrm{54}\right)={sin}\left(\mathrm{162}\right)={sin}\left(\mathrm{180}−\mathrm{18}\right)={sin}\mathrm{18} \\ $$$${RHS}\:−{cos}\left(\mathrm{108}\right)=−{cos}\left(\mathrm{90}+\mathrm{18}\right)=−\left(−{sin}\mathrm{18}\right)={sin}\mathrm{18} \\ $$$${so}\:{sin}\mathrm{3}\theta=−{cos}\mathrm{2}\theta\:{proved} \\ $$$${sin}\mathrm{54}=\mathrm{3}{sin}\mathrm{18}−\mathrm{4}{sin}^{\mathrm{3}} \mathrm{18} \\ $$$${sin}\mathrm{54}=\mathrm{3}\left(\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{4}}\right)−\mathrm{4}\left(\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} \\ $$

Answered by $@y@m last updated on 13/Nov/20

(i) sin (x+y)=sin xcos y+cos xsin y Put x=2A, y=A sin 3A=sin 2Acos A+cos 2Asin A =(2sinAcos A)cos A+(1−2sin^2 A)sin A =2sinAcos^2 A+sin A−2sin^3 A =2sinA(1−sin^2 A)+sin A−2sin^3 A =2sinA−2sin^3 A+sin A−2sin^3 A =3sinA−4sin^3 A ■■■ (ii) sin (3×54)=sin 162=sin (180−18)=sin 18 −cos (2×54)=−cos 108=−cos (90+18)=sin 18 ■■■ sin 54=sin (3×18) =3sin 18−4sin^3 18 =sin 18(3−4sin^2 18) = (((√5)−1)/4){3−4×((5+1−2(√5))/(16))} = (((√5)−1)/4){3−((6−2(√5))/4)} = (((√5)−1)/4)×((6+2(√5))/4) = ((6(√5)−6+10−2(√5))/(16)) = ((4+4(√5))/(16)) =(((√5)+1)/4)

$$\left({i}\right)\:\mathrm{sin}\:\left({x}+{y}\right)=\mathrm{sin}\:{x}\mathrm{cos}\:{y}+\mathrm{cos}\:{x}\mathrm{sin}\:{y} \\ $$$${Put}\:{x}=\mathrm{2}{A},\:{y}={A} \\ $$$$\mathrm{sin}\:\mathrm{3}{A}=\mathrm{sin}\:\mathrm{2}{A}\mathrm{cos}\:{A}+\mathrm{cos}\:\mathrm{2}{A}\mathrm{sin}\:{A} \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{2sin}{A}\mathrm{cos}\:{A}\right)\mathrm{cos}\:{A}+\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {A}\right)\mathrm{sin}\:{A} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2sin}{A}\mathrm{cos}^{\mathrm{2}} {A}+\mathrm{sin}\:{A}−\mathrm{2sin}^{\mathrm{3}} {A} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2sin}{A}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {A}\right)+\mathrm{sin}\:{A}−\mathrm{2sin}^{\mathrm{3}} {A} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2sin}{A}−\mathrm{2sin}^{\mathrm{3}} {A}+\mathrm{sin}\:{A}−\mathrm{2sin}^{\mathrm{3}} {A} \\ $$$$\:\:\:\:\:\:\:=\mathrm{3sin}{A}−\mathrm{4sin}^{\mathrm{3}} {A}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\blacksquare\blacksquare\blacksquare \\ $$$$\left({ii}\right)\:\mathrm{sin}\:\left(\mathrm{3}×\mathrm{54}\right)=\mathrm{sin}\:\mathrm{162}=\mathrm{sin}\:\left(\mathrm{180}−\mathrm{18}\right)=\mathrm{sin}\:\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:−\mathrm{cos}\:\left(\mathrm{2}×\mathrm{54}\right)=−\mathrm{cos}\:\mathrm{108}=−\mathrm{cos}\:\left(\mathrm{90}+\mathrm{18}\right)=\mathrm{sin}\:\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\blacksquare\blacksquare\blacksquare \\ $$$$\mathrm{sin}\:\mathrm{54}=\mathrm{sin}\:\left(\mathrm{3}×\mathrm{18}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3sin}\:\mathrm{18}−\mathrm{4sin}\:^{\mathrm{3}} \mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{sin}\:\mathrm{18}\left(\mathrm{3}−\mathrm{4sin}^{\mathrm{2}} \mathrm{18}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\left\{\mathrm{3}−\mathrm{4}×\frac{\mathrm{5}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\left\{\mathrm{3}−\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{6}\sqrt{\mathrm{5}}−\mathrm{6}+\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{4}+\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$

Commented by ZiYangLee last updated on 16/Nov/20

thanks!

$$\mathrm{thanks}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com