Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 122071 by bemath last updated on 13/Nov/20

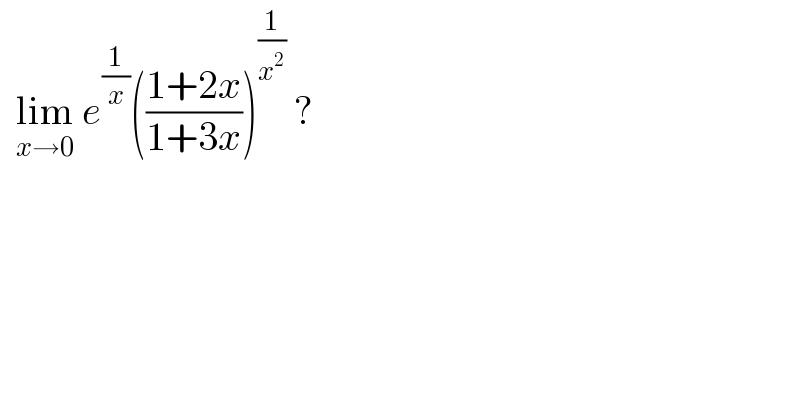
lim_(x→0) e^(1/x) (((1+2x)/(1+3x)))^(1/x^2 ) ?

$$\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{e}^{\frac{\mathrm{1}}{{x}}} \left(\frac{\mathrm{1}+\mathrm{2}{x}}{\mathrm{1}+\mathrm{3}{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:? \\ $$

Answered by liberty last updated on 13/Nov/20

L = lim_(x→0) e^(1/x) (((1+2x)/(1+3x)))^(1/x^2 ) L = e^(lim_(x→0) ℓn(e^(1/x) .(((1+2x)/(1+3x)))^(1/x^2 ) )) L = e^(lim_(x→0) ((1/x)+((ℓn(((1+2x)/(1+3x)) ))/x^2 ))) L = e^(lim_(x→0) (((x+ℓn(((1+2x)/(1+3x))))/x^2 ))) L = e^(lim_(x→0) (((1+(((1+3x)/(1+2x))).(((−1)/((1+3x)^2 ))))/(2x)))) L = e^(lim_(x→0) (((1−(1/((1+5x+6x^2 ))))/(2x)))) = e^(lim_(x→0) (((1−(1+5x+6x^2 )^(−1) )/(2x)))) L=e^(lim_(x→0) ((((5+12x))/(2(1+5x+6x^2 )^2 )))) = e^(5/2) = (√e^5 ). ▲

$$\:\mathrm{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \:\left(\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\mathrm{3x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\ell\mathrm{n}\left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} .\left(\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\mathrm{3x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \right)} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}\:^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{x}}+\frac{\ell\mathrm{n}\left(\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\mathrm{3x}}\:\right)}{\mathrm{x}^{\mathrm{2}} }\right)} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{x}+\ell\mathrm{n}\left(\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\mathrm{3x}}\right)}{\mathrm{x}^{\mathrm{2}} }\right)} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}+\left(\frac{\mathrm{1}+\mathrm{3x}}{\mathrm{1}+\mathrm{2x}}\right).\left(\frac{−\mathrm{1}}{\left(\mathrm{1}+\mathrm{3x}\right)^{\mathrm{2}} }\right)}{\mathrm{2x}}\right)} \\ $$$$\:\mathrm{L}\:=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{5x}+\mathrm{6x}^{\mathrm{2}} \right)}}{\mathrm{2x}}\right)} \:=\:\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}−\left(\mathrm{1}+\mathrm{5x}+\mathrm{6x}^{\mathrm{2}} \right)^{−\mathrm{1}} }{\mathrm{2x}}\right)} \\ $$$$\:\mathrm{L}=\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\mathrm{5}+\mathrm{12x}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{5x}+\mathrm{6x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right)} \:=\:\mathrm{e}^{\frac{\mathrm{5}}{\mathrm{2}}} \:=\:\sqrt{\mathrm{e}^{\mathrm{5}} }.\:\blacktriangle \\ $$

Answered by mathmax by abdo last updated on 14/Nov/20

let L(x)=e^(1/x) (((1+2x)/(1+3x)))^(1/x^2 ) ⇒L(x)=e^(1/x) e^((1/x^2 )ln(((1+2x)/(1+3x)))) =e^((1/x)+(1/x^2 )ln(((2x+1)/(3x+1)))) we have ln(((2x+1)/(3x+1))) =ln(1+2x)−ln(1+3x) ln^′ (1+u) =(1/(1+u)) =1−u +o(u^2 ) ⇒ln(1+u)∼u−(u^2 /2) ⇒ ln(1+2x)∼2x−(((2x)^2 )/2)=2x−2x^2 and ln(1+3x)∼3x−(((3x)^2 )/2) =3x−(9/2)x^2 ⇒ln(1+2x)−ln(1+3x)∼2x−2x^2 −3x+(9/2)x^2 =−x +(5/2)x^2 ⇒(1/x^2 )ln(((1+2x)/(1+3x))) ∼−(1/x)+(5/2) ⇒ (1/x)+(1/x^2 )ln(((1+2x)/(1+3x))) ∼(5/2) ⇒lim_(x→0) L(x) =e^(5/2) =(√e^5 )

$$\mathrm{let}\:\mathrm{L}\left(\mathrm{x}\right)=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \left(\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\mathrm{3x}}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:\Rightarrow\mathrm{L}\left(\mathrm{x}\right)=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\mathrm{3x}}\right)} \\ $$$$=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{3x}+\mathrm{1}}\right)} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{ln}\left(\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{3x}+\mathrm{1}}\right)\:=\mathrm{ln}\left(\mathrm{1}+\mathrm{2x}\right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{3x}\right) \\ $$$$\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\mathrm{1}−\mathrm{u}\:+\mathrm{o}\left(\mathrm{u}^{\mathrm{2}} \right)\:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)\sim\mathrm{u}−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{2x}\right)\sim\mathrm{2x}−\frac{\left(\mathrm{2x}\right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2x}−\mathrm{2x}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{ln}\left(\mathrm{1}+\mathrm{3x}\right)\sim\mathrm{3x}−\frac{\left(\mathrm{3x}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\mathrm{3x}−\frac{\mathrm{9}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{2x}\right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{3x}\right)\sim\mathrm{2x}−\mathrm{2x}^{\mathrm{2}} −\mathrm{3x}+\frac{\mathrm{9}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \\ $$$$=−\mathrm{x}\:+\frac{\mathrm{5}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \:\:\Rightarrow\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\mathrm{3x}}\right)\:\sim−\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{5}}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\mathrm{3x}}\right)\:\sim\frac{\mathrm{5}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{L}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{5}}{\mathrm{2}}} \:\:=\sqrt{\mathrm{e}^{\mathrm{5}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com