
Question and Answers Forum
Question Number 122106 by bemath last updated on 14/Nov/20
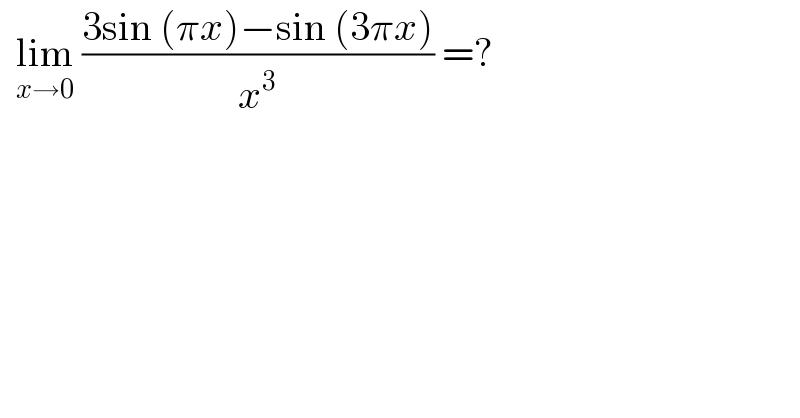
Answered by liberty last updated on 14/Nov/20
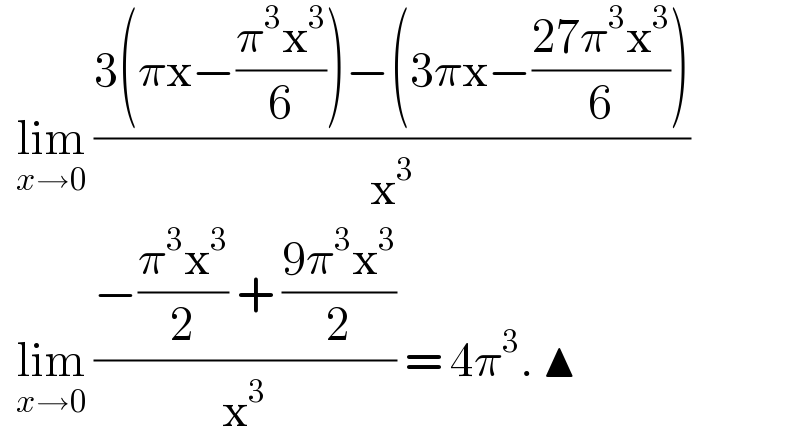
Answered by Bird last updated on 14/Nov/20
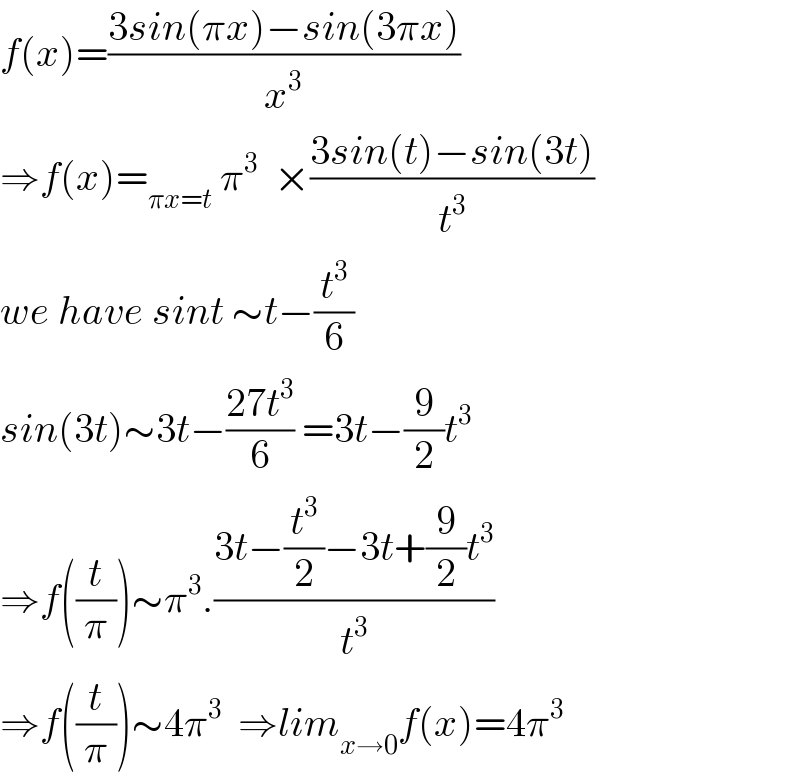
| ||
Question and Answers Forum | ||
Question Number 122106 by bemath last updated on 14/Nov/20 | ||
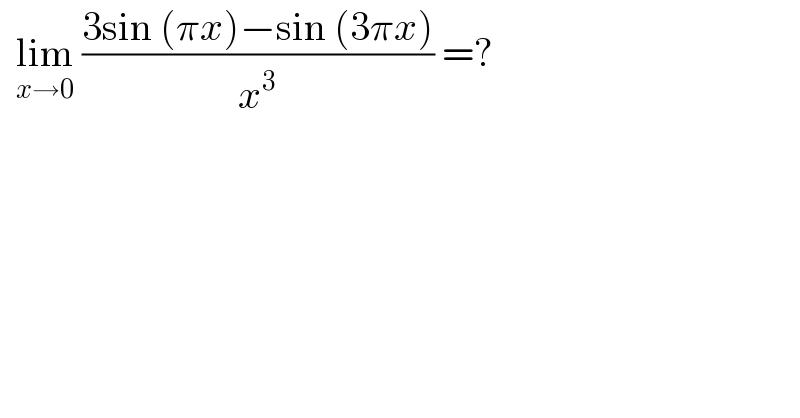 | ||
Answered by liberty last updated on 14/Nov/20 | ||
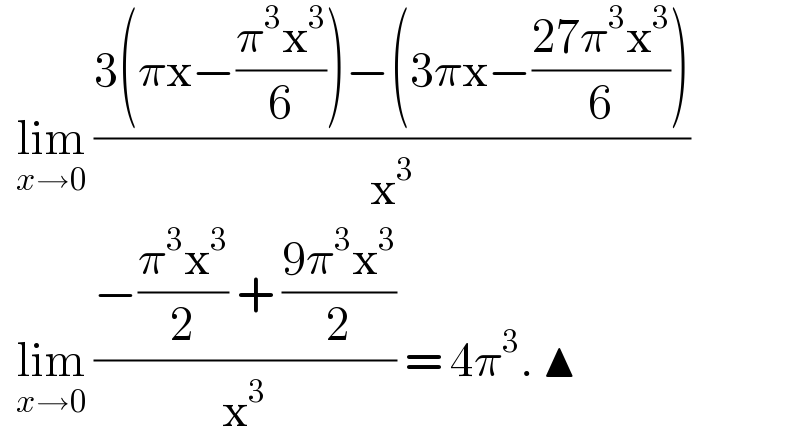 | ||
| ||
Answered by Bird last updated on 14/Nov/20 | ||
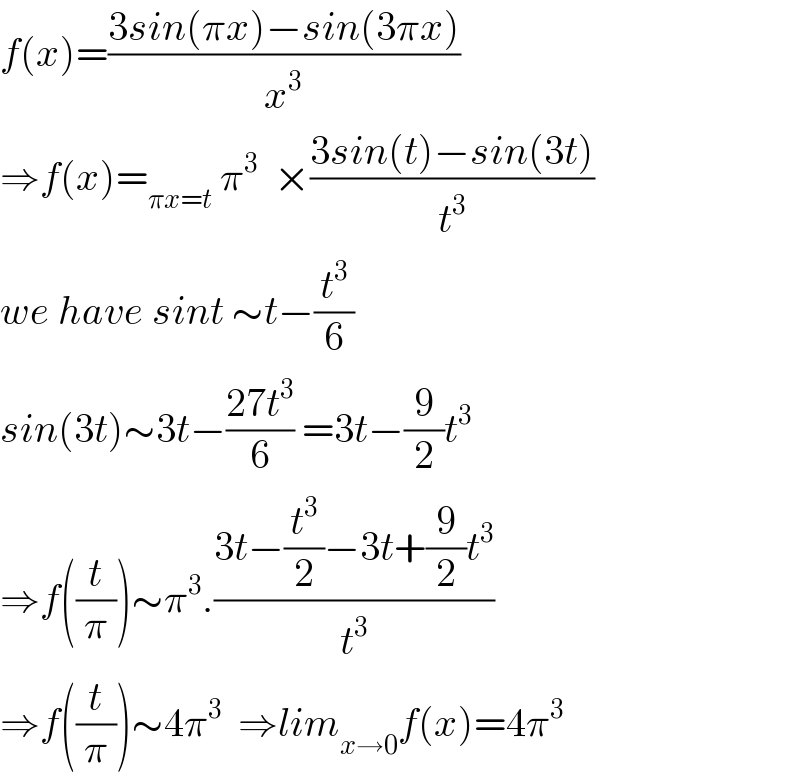 | ||
| ||