
Question Number 122162 by naka3546 last updated on 14/Nov/20
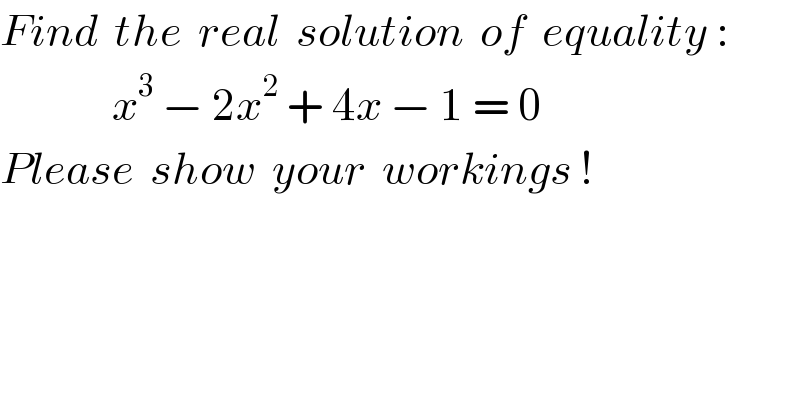
$${Find}\:\:{the}\:\:{real}\:\:{solution}\:\:{of}\:\:{equality}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{3}} \:−\:\mathrm{2}{x}^{\mathrm{2}} \:+\:\mathrm{4}{x}\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$${Please}\:\:{show}\:\:{your}\:\:{workings}\:! \\ $$
Answered by mathmax by abdo last updated on 14/Nov/20
![f(x)=x^3 −2x^2 +4x−1 ⇒f^′ (x)=3x^2 −4x+4 f^′ (x)=0 ⇒3x^2 −4x+4 =0 →Δ^′ =4−12 =−8<0 a=3>0 ⇒f^′ (x)>0 ⇒f is strictly increasing on R f(0)=−1 and f(1) =1−2+4−1 =2>0 f(0).f(−1)<0 ⇒∃!α ∈]0,1[ /f(α)=0 let begin by x_0 =(1/2) and x_(n+1) =x_n −((f(x_n ))/(f^′ (x_n ))) (newton method) x_1 =x_0 −((f(x_0 ))/(f^′ (x_0 ))) =(1/2)−((f((1/2)))/(f^′ ((1/2)))) we have f((1/2))=(1/8)−(1/2) +2−1 =((1−4)/8) +1 =((−3)/8) +1 =(5/8) f^′ ((1/2))=(3/4)−2 +4 =(3/4)+2 =((11)/4) ⇒x_1 =(1/2)−(5/8)×(4/(11)) =(1/2)−(5/(22)) =((11−5)/(22)) =(6/(22)) =(3/(11)) x_2 =x_1 −((f(x_1 ))/(f^′ (x_1 )))=(3/(11))−((f((3/(11))))/(f^′ ((3/(11))))) =... x_4 give a better approximation to this root...](Q122206.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{4x}−\mathrm{1}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)=\mathrm{3x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}\: \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\mathrm{0}\:\Rightarrow\mathrm{3x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{4}−\mathrm{12}\:=−\mathrm{8}<\mathrm{0} \\ $$$$\mathrm{a}=\mathrm{3}>\mathrm{0}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)>\mathrm{0}\:\Rightarrow\mathrm{f}\:\mathrm{is}\:\mathrm{strictly}\:\mathrm{increasing}\:\mathrm{on}\:\mathrm{R} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=−\mathrm{1}\:\mathrm{and}\:\mathrm{f}\left(\mathrm{1}\right)\:=\mathrm{1}−\mathrm{2}+\mathrm{4}−\mathrm{1}\:=\mathrm{2}>\mathrm{0}\: \\ $$$$\left.\mathrm{f}\left(\mathrm{0}\right).\mathrm{f}\left(−\mathrm{1}\right)<\mathrm{0}\:\Rightarrow\exists!\alpha\:\in\right]\mathrm{0},\mathrm{1}\left[\:\:/\mathrm{f}\left(\alpha\right)=\mathrm{0}\:\:\mathrm{let}\:\mathrm{begin}\:\mathrm{by}\:\mathrm{x}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\right. \\ $$$$\mathrm{and}\:\:\mathrm{x}_{\mathrm{n}+\mathrm{1}} =\mathrm{x}_{\mathrm{n}} −\frac{\mathrm{f}\left(\mathrm{x}_{\mathrm{n}} \right)}{\mathrm{f}^{'} \left(\mathrm{x}_{\mathrm{n}} \right)}\:\:\:\:\:\left(\mathrm{newton}\:\mathrm{method}\right) \\ $$$$\mathrm{x}_{\mathrm{1}} =\mathrm{x}_{\mathrm{0}} −\frac{\mathrm{f}\left(\mathrm{x}_{\mathrm{0}} \right)}{\mathrm{f}^{'} \left(\mathrm{x}_{\mathrm{0}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{2}−\mathrm{1} \\ $$$$=\frac{\mathrm{1}−\mathrm{4}}{\mathrm{8}}\:+\mathrm{1}\:=\frac{−\mathrm{3}}{\mathrm{8}}\:+\mathrm{1}\:=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\mathrm{f}^{'} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{2}\:+\mathrm{4}\:=\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{2}\:=\frac{\mathrm{11}}{\mathrm{4}}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{8}}×\frac{\mathrm{4}}{\mathrm{11}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{22}}\:=\frac{\mathrm{11}−\mathrm{5}}{\mathrm{22}}\:=\frac{\mathrm{6}}{\mathrm{22}}\:=\frac{\mathrm{3}}{\mathrm{11}} \\ $$$$\mathrm{x}_{\mathrm{2}} =\mathrm{x}_{\mathrm{1}} −\frac{\mathrm{f}\left(\mathrm{x}_{\mathrm{1}} \right)}{\mathrm{f}^{'} \left(\mathrm{x}_{\mathrm{1}} \right)}=\frac{\mathrm{3}}{\mathrm{11}}−\frac{\mathrm{f}\left(\frac{\mathrm{3}}{\mathrm{11}}\right)}{\mathrm{f}^{'} \left(\frac{\mathrm{3}}{\mathrm{11}}\right)}\:=... \\ $$$$\mathrm{x}_{\mathrm{4}} \:\mathrm{give}\:\mathrm{a}\:\mathrm{better}\:\mathrm{approximation}\:\mathrm{to}\:\mathrm{this}\:\mathrm{root}... \\ $$
