Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 122166 by physicstutes last updated on 14/Nov/20

$$\mathrm{Given}\mathrm{that}{I}_n=\underset{0}{\stackrel{1}{\int }}x{(1-x)}^{n}dx$$$$\mathrm{obtain}\mathrm{a}\mathrm{reduction}\mathrm{formulae}\mathrm{for}{I}_n\mathrm{in}\mathrm{terms}$$$$\mathrm{of}{I}_{n-2}\mathrm{Hence}\mathrm{evaluate}\underset{0}{\stackrel{1}{\int }}x{(1-x)}^{5}dx.$$

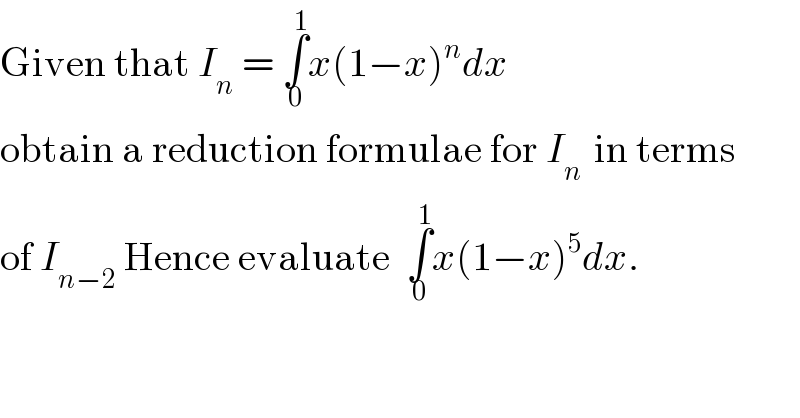
Answered by liberty last updated on 14/Nov/20

$${\underset{0}{\stackrel{1}{\int }}\mathrm{x}{(1-\mathrm{x})}^5\mathrm{dx}=-\frac{\mathrm{x}{(1-\mathrm{x})}^6}{6}]}_0^1+\underset{0}{\stackrel{1}{\int }}\frac{{(1-\mathrm{x})}^6}{6}\mathrm{dx}$$$$=-\frac{1}{42}{\left[(1-\mathrm{x})\right]}_0^1=\frac{1}{42}$$

Commented by physicstutes last updated on 14/Nov/20

$$\mathrm{from}\mathrm{your}\mathrm{method}\mathrm{i}\mathrm{deduce}\mathrm{that}:$$$$I_n=-{\left[\frac{x{(1-x)}^{n+1}}{n+1}\right]}_0^1+\underset{0}{\stackrel{1}{\int }}\frac{{(1-x)}^{n+1}}{n+1}dx$$$$I_n=\frac{1}{n+1}\underset{0}{\stackrel{1}{\int }}{(1-x)}^{n+1}dx$$$$\mathrm{Thanks}$$

Commented by Dwaipayan Shikari last updated on 14/Nov/20

$${\int }_0^{1}x{(1-x)}^{n}dx={\int }_0^1(1-x)x^{n}dx=\frac{1}{n+1}-\frac{1}{n+2}$$$$heren=5so,\frac{1}{42}$$

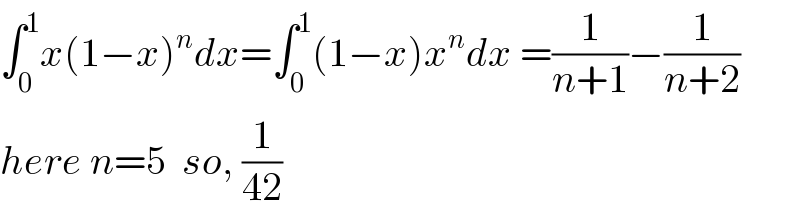
Answered by Dwaipayan Shikari last updated on 14/Nov/20

$${\int }_0^{1}x{(1-x)}^{n}dx$$$$=\beta (2,n+1)=\frac{\mathrm{\Gamma }\left(2\right)\mathrm{\Gamma }(n+1)}{\mathrm{\Gamma }(n+3)}=\frac{\mathrm{\Gamma }(n+1)}{\mathrm{\Gamma }(n+3)}$$$$So$$$${\int }_0^{1}x{(1-x)}^{5}dt=\frac{\mathrm{\Gamma }(5+1)}{\mathrm{\Gamma }(5+3)}=\frac{5!}{7!}=\frac{1}{42}$$

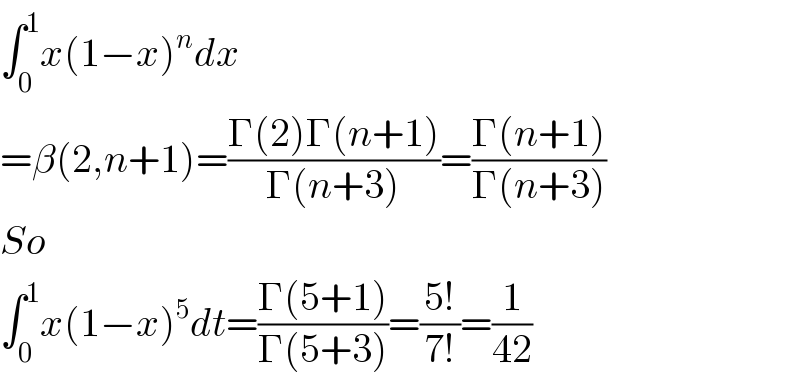
Commented by physicstutes last updated on 14/Nov/20

$$\mathrm{Magnifcent}!$$

Answered by mathmax by abdo last updated on 14/Nov/20

$${\mathrm{I}}_{\mathrm{n}}={\int }_0^1\mathrm{x}{(1-\mathrm{x})}^{\mathrm{n}}\mathrm{dx}\mathrm{we}\mathrm{know}\mathrm{B}(\mathrm{p},\mathrm{q})={\int }_0^1{\mathrm{x}}^{\mathrm{p}-1}{(1-\mathrm{x})}^{\mathrm{q}-1}\mathrm{dx}\Rightarrow$$$$\mathrm{B}(\mathrm{p},\mathrm{q})=\frac{\mathrm{\Gamma }\left(\mathrm{p}\right).\mathrm{\Gamma }\left(\mathrm{q}\right)}{\mathrm{\Gamma }(\mathrm{p}+\mathrm{q})}\Rightarrow {\mathrm{I}}_{\mathrm{n}}={\int }_0^1{\mathrm{x}}^{2-1}{(1-\mathrm{x})}^{\mathrm{n}+1-1}\mathrm{dx}=\mathrm{B}(2,\mathrm{n}+1)$$$$=\frac{\mathrm{\Gamma }\left(2\right).\mathrm{\Gamma }(\mathrm{n}+1)}{\mathrm{\Gamma }(2+\mathrm{n}+1)}=\frac{1!\mathrm{n}!}{(\mathrm{n}+2)!}=\frac{\mathrm{n}!}{(\mathrm{n}+2)(\mathrm{n}+1)\mathrm{n}!}=\frac{1}{(\mathrm{n}+1)(\mathrm{n}+2)}$$$$\frac{{\mathrm{I}}_{\mathrm{n}}}{{\mathrm{I}}_{\mathrm{n}-2}}=\frac{1}{(\mathrm{n}+1)(\mathrm{n}+2)}.(\mathrm{n}-1)\mathrm{n}=\frac{\mathrm{n}(\mathrm{n}-1)}{(\mathrm{n}+1)(\mathrm{n}+2)}\Rightarrow$$$${\mathrm{I}}_{\mathrm{n}}=\frac{\mathrm{n}(\mathrm{n}-1)}{(\mathrm{n}+1)(\mathrm{n}+2)}{\mathrm{I}}_{\mathrm{n}-2}(\mathrm{n}⩾2)$$$${\int }_0^1\mathrm{x}{(1-\mathrm{x})}^5\mathrm{dx}={\mathrm{I}}_5=\frac{1}{6.7}=\frac{1}{42}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com