Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 122185 by mnjuly1970 last updated on 14/Nov/20

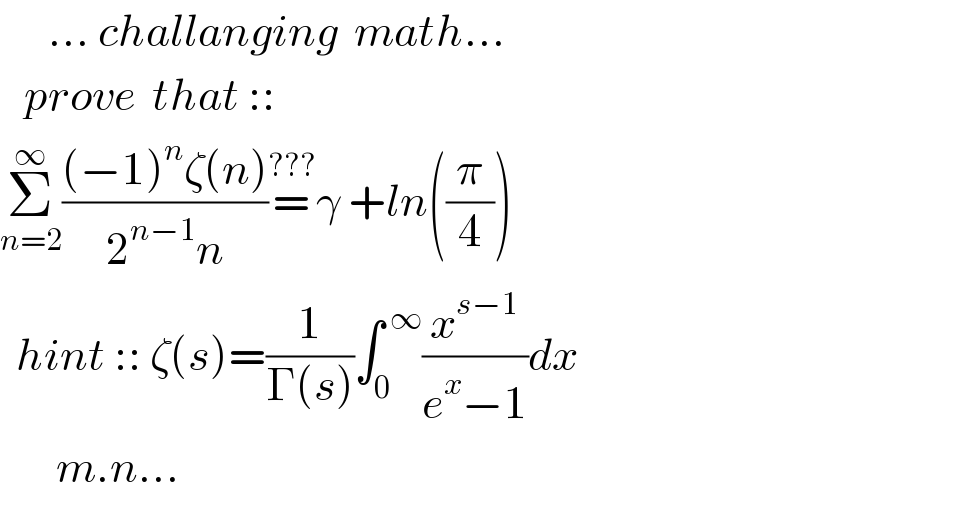
... challanging math... prove that :: Σ_(n=2) ^∞ (((−1)^n ζ(n))/(2^(n−1) n))=^(???) γ +ln((π/4)) hint :: ζ(s)=(1/(Γ(s)))∫_0 ^( ∞) (x^(s−1) /(e^x −1))dx m.n...

$$\:\:\:\:\:\:...\:{challanging}\:\:{math}... \\ $$$$\:\:\:{prove}\:\:{that}\::: \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \zeta\left({n}\right)}{\mathrm{2}^{{n}−\mathrm{1}} {n}}\overset{???} {=}\gamma\:+{ln}\left(\frac{\pi}{\mathrm{4}}\right)\: \\ $$$$\:\:{hint}\:::\:\zeta\left({s}\right)=\frac{\mathrm{1}}{\Gamma\left({s}\right)}\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{{s}−\mathrm{1}} }{{e}^{{x}} −\mathrm{1}}{dx} \\ $$$$\:\:\:\:\:\:\:{m}.{n}... \\ $$

Commented by Dwaipayan Shikari last updated on 15/Nov/20

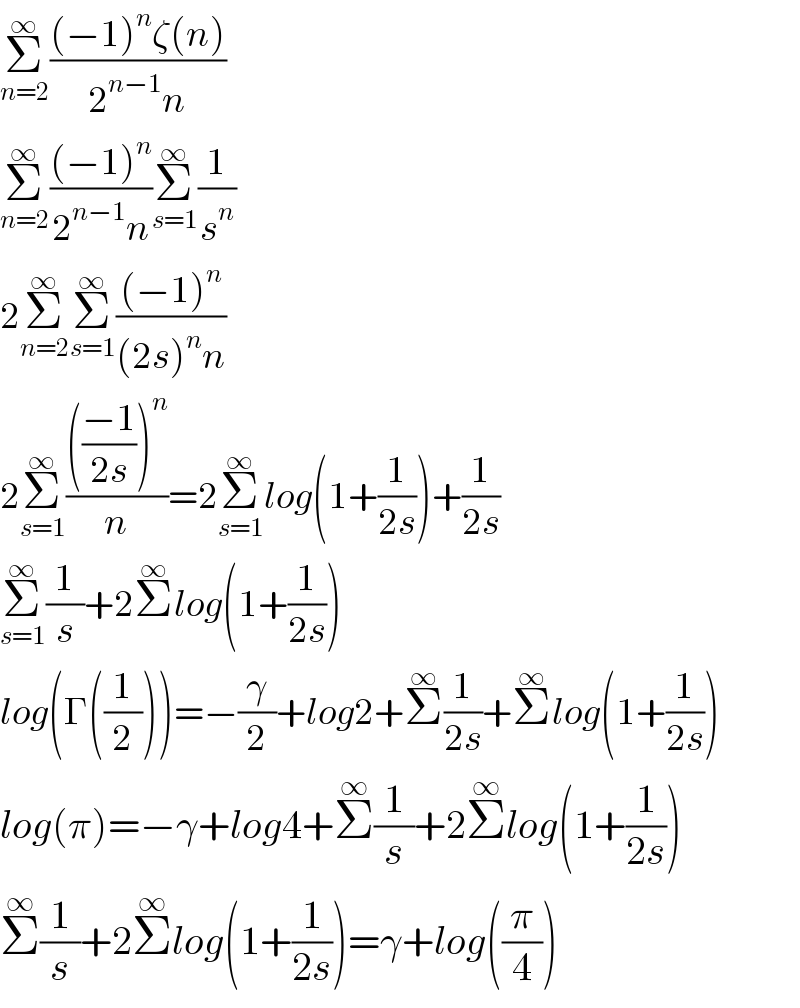
Σ_(n=2) ^∞ (((−1)^n ζ(n))/(2^(n−1) n)) Σ_(n=2) ^∞ (((−1)^n )/(2^(n−1) n))Σ_(s=1) ^∞ (1/s^n ) 2Σ_(n=2) ^∞ Σ_(s=1) ^∞ (((−1)^n )/((2s)^n n)) 2Σ_(s=1) ^∞ (((((−1)/(2s)))^n )/n)=2Σ_(s=1) ^∞ log(1+(1/(2s)))+(1/(2s)) Σ_(s=1) ^∞ (1/s)+2Σ^∞ log(1+(1/(2s))) log(Γ((1/2)))=−(γ/2)+log2+Σ^∞ (1/(2s))+Σ^∞ log(1+(1/(2s))) log(π)=−γ+log4+Σ^∞ (1/s)+2Σ^∞ log(1+(1/(2s))) Σ^∞ (1/s)+2Σ^∞ log(1+(1/(2s)))=γ+log((π/4))

$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \zeta\left({n}\right)}{\mathrm{2}^{{n}−\mathrm{1}} {n}} \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}−\mathrm{1}} {n}}\underset{{s}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{s}^{{n}} } \\ $$$$\mathrm{2}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\underset{{s}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{s}\right)^{{n}} {n}} \\ $$$$\mathrm{2}\underset{{s}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\frac{−\mathrm{1}}{\mathrm{2}{s}}\right)^{{n}} }{{n}}=\mathrm{2}\underset{{s}=\mathrm{1}} {\overset{\infty} {\sum}}{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{s}}\right)+\frac{\mathrm{1}}{\mathrm{2}{s}} \\ $$$$\underset{{s}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{s}}+\mathrm{2}\overset{\infty} {\sum}{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{s}}\right) \\ $$$${log}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=−\frac{\gamma}{\mathrm{2}}+{log}\mathrm{2}+\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{2}{s}}+\overset{\infty} {\sum}{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{s}}\right) \\ $$$${log}\left(\pi\right)=−\gamma+{log}\mathrm{4}+\overset{\infty} {\sum}\frac{\mathrm{1}}{{s}}+\mathrm{2}\overset{\infty} {\sum}{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{s}}\right) \\ $$$$\overset{\infty} {\sum}\frac{\mathrm{1}}{{s}}+\mathrm{2}\overset{\infty} {\sum}{log}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{s}}\right)=\gamma+{log}\left(\frac{\pi}{\mathrm{4}}\right) \\ $$

Commented by mnjuly1970 last updated on 15/Nov/20

very nice .bravo master dwaipayan..

$${very}\:{nice}\:.{bravo} \\ $$$$\:\:{master}\:\:{dwaipayan}.. \\ $$

Answered by mindispower last updated on 15/Nov/20

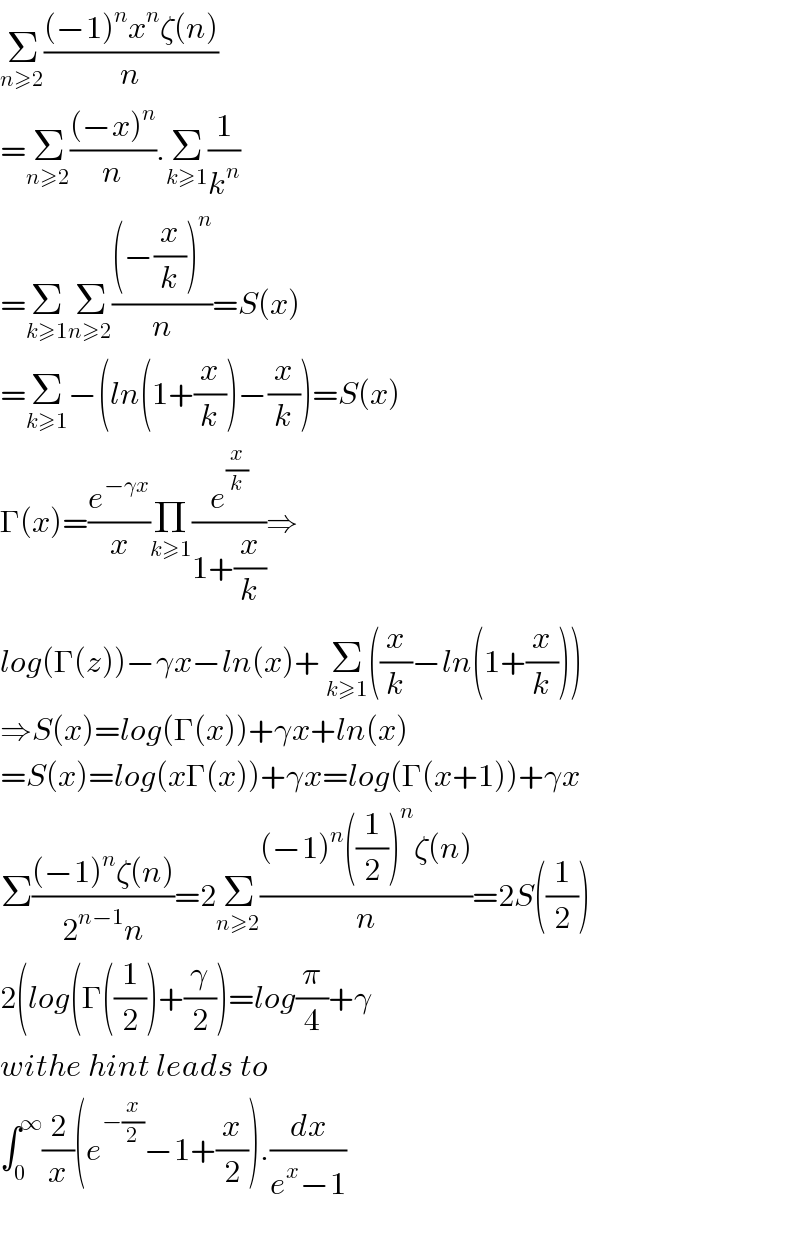
Σ_(n≥2) (((−1)^n x^n ζ(n))/n) =Σ_(n≥2) (((−x)^n )/n).Σ_(k≥1) (1/k^n ) =Σ_(k≥1) Σ_(n≥2) (((−(x/k))^n )/n)=S(x) =Σ_(k≥1) −(ln(1+(x/k))−(x/k))=S(x) Γ(x)=(e^(−γx) /x)Π_(k≥1) (e^(x/k) /(1+(x/k)))⇒ log(Γ(z))−γx−ln(x)+ Σ_(k≥1) ((x/k)−ln(1+(x/k))) ⇒S(x)=log(Γ(x))+γx+ln(x) =S(x)=log(xΓ(x))+γx=log(Γ(x+1))+γx Σ(((−1)^n ζ(n))/(2^(n−1) n))=2Σ_(n≥2) (((−1)^n ((1/2))^n ζ(n))/n)=2S((1/2)) 2(log(Γ((1/2))+(γ/2))=log(π/4)+γ withe hint leads to ∫_0 ^∞ (2/x)(e^(−(x/2)) −1+(x/2)).(dx/(e^x −1))

$$\underset{{n}\geqslant\mathrm{2}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \zeta\left({n}\right)}{{n}} \\ $$$$=\underset{{n}\geqslant\mathrm{2}} {\sum}\frac{\left(−{x}\right)^{{n}} }{{n}}.\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{k}^{{n}} } \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\underset{{n}\geqslant\mathrm{2}} {\sum}\frac{\left(−\frac{{x}}{{k}}\right)^{{n}} }{{n}}={S}\left({x}\right) \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}−\left({ln}\left(\mathrm{1}+\frac{{x}}{{k}}\right)−\frac{{x}}{{k}}\right)={S}\left({x}\right) \\ $$$$\Gamma\left({x}\right)=\frac{{e}^{−\gamma{x}} }{{x}}\underset{{k}\geqslant\mathrm{1}} {\prod}\frac{{e}^{\frac{{x}}{{k}}} }{\mathrm{1}+\frac{{x}}{{k}}}\Rightarrow \\ $$$${log}\left(\Gamma\left({z}\right)\right)−\gamma{x}−{ln}\left({x}\right)+\:\underset{{k}\geqslant\mathrm{1}} {\sum}\left(\frac{{x}}{{k}}−{ln}\left(\mathrm{1}+\frac{{x}}{{k}}\right)\right) \\ $$$$\Rightarrow{S}\left({x}\right)={log}\left(\Gamma\left({x}\right)\right)+\gamma{x}+{ln}\left({x}\right) \\ $$$$={S}\left({x}\right)={log}\left({x}\Gamma\left({x}\right)\right)+\gamma{x}={log}\left(\Gamma\left({x}+\mathrm{1}\right)\right)+\gamma{x} \\ $$$$\Sigma\frac{\left(−\mathrm{1}\right)^{{n}} \zeta\left({n}\right)}{\mathrm{2}^{{n}−\mathrm{1}} {n}}=\mathrm{2}\underset{{n}\geqslant\mathrm{2}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \zeta\left({n}\right)}{{n}}=\mathrm{2}{S}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{2}\left({log}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\gamma}{\mathrm{2}}\right)={log}\frac{\pi}{\mathrm{4}}+\gamma\right. \\ $$$${withe}\:{hint}\:{leads}\:{to} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}}{{x}}\left({e}^{−\frac{{x}}{\mathrm{2}}} −\mathrm{1}+\frac{{x}}{\mathrm{2}}\right).\frac{{dx}}{{e}^{{x}} −\mathrm{1}} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 15/Nov/20

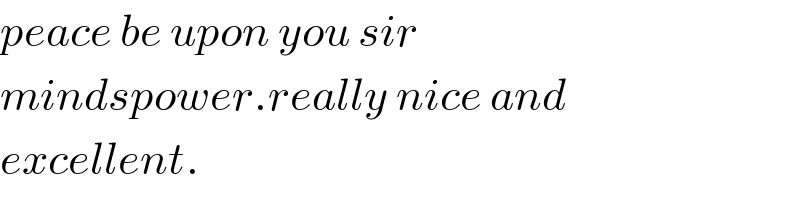
peace be upon you sir mindspower.really nice and excellent.

$${peace}\:{be}\:{upon}\:{you}\:{sir}\: \\ $$$${mindspower}.{really}\:{nice}\:{and} \\ $$$${excellent}. \\ $$

Answered by mnjuly1970 last updated on 15/Nov/20

Answered by mnjuly1970 last updated on 15/Nov/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com