Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 122186 by physicstutes last updated on 14/Nov/20

$$\mathrm{Obtain}\mathrm{a}\mathrm{reduction}\mathrm{formulae}\mathrm{for}$$$$I_n=\underset{0}{\stackrel{1}{\int }}{\left(\ln x\right)}^{n}dx$$$$\mathrm{find}{I}_2=\underset{0}{\stackrel{1}{\int }}{\left(\ln x\right)}^{2}dx$$

Answered by Olaf last updated on 14/Nov/20

$${\mathrm{I}}_n={\int }_0^1{\ln }^{n}xdx$$$${\mathrm{I}}_0=1\mathrm{and}\mathrm{for}n⩾1:$$$${\mathrm{I}}_n={\left[x{\ln }^{n}x\right]}_0^1-{\int }_0^{1}x\left(n\frac{1}{x}{\ln }^{n-1}x\right)dx$$$${\mathrm{I}}_n=-n{\int }_0^1{\ln }^{n-1}xdx=-n{\mathrm{I}}_{n-1}$$$$\Rightarrow {\mathrm{I}}_n={(-1)}^{n}n!{\mathrm{I}}_0={(-1)}^{n}n!$$$$\mathrm{If}n=2,{\mathrm{I}}_2={(-1)}^{2}2!=2$$

Commented by physicstutes last updated on 14/Nov/20

$$\mathrm{This}\mathrm{is}\mathrm{incredible}.\mathrm{Thank}\mathrm{you}\mathrm{sir}\mathrm{Olaf}.$$

Answered by Dwaipayan Shikari last updated on 14/Nov/20

$${\int }_{\mathrm{\infty }}^0{t}^{n}xdtlogx=t\Rightarrow \frac{1}{x}=\frac{dt}{dx}$$$$={\int }_{\mathrm{\infty }}^0{t}^n{e}^{t}dt$$$$={\int }_0^{\mathrm{\infty }}{(-1)}^n{u}^n{e}^{-t}dtt=-u$$$$={(-1)}^n\mathrm{\Gamma }(n+1)={(-1)}^{n}n!$$$$asperquestion$$$$Itis{(-1)}^{2}2!=2$$

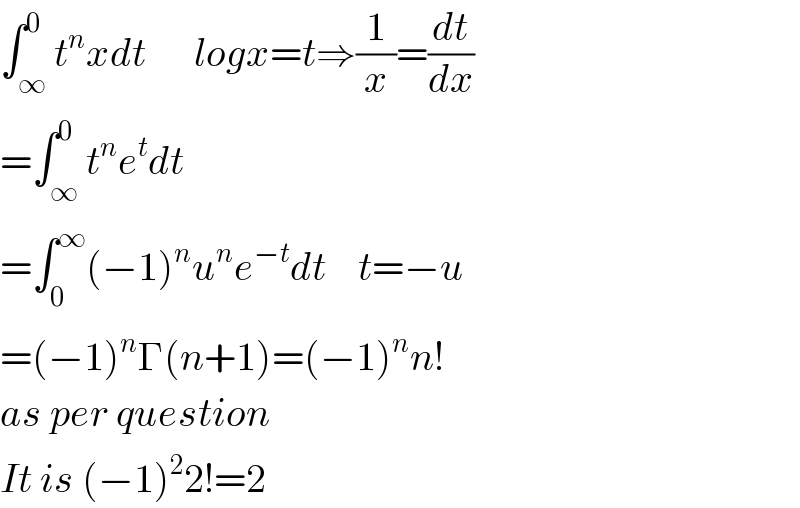
Commented by physicstutes last updated on 14/Nov/20

$$\mathrm{thats}\mathrm{right}!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com