
Question and Answers Forum
Question Number 122205 by mathmax by abdo last updated on 14/Nov/20
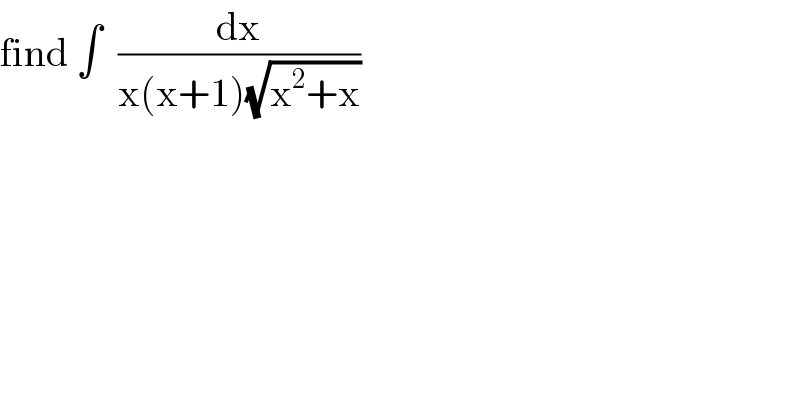
Commented by liberty last updated on 15/Nov/20
![∫ (dx/((x^2 +x)^(3/2) )) = ∫ (dx/(x^3 (1+x^(−1) )^(3/2) )) = ∫ ((x^(−2) dx)/(x(1+x^(−1) )^(3/2) )) ; [ u^(2/3) = 1+(1/x) ] ⇒ [ (2/3)u^(−(1/3)) du = −x^(−2) dx ] J = ∫ (u^(2/3) −1)(−(2/3)u^(−(1/3)) du)((1/u)) J= −(2/3)∫ (u^(2/3) −1)(u^(−(4/3)) ) du J=−(2/3)∫ (u^(−(2/3)) −u^(−(4/3)) ) du J = −(2/3)[ 3u^(1/3) +3u^(−(1/3)) ] + c J = −2(√((x+1)/x))−2(√(x/(x+1))) + c J= −2(((x+1+x)/( (√(x^2 +x)))))+ c = −((4x+2)/( (√(x^2 +x)))) + c](Q122225.png)
Commented by benjo_mathlover last updated on 15/Nov/20
![let J(x)=−((4x+2)/( (√(x^2 +x)))) ((dJ(x))/dx) = − [ ((4(√(x^2 +x))−(4x+2)(((2x+1)/(2(√(x^2 +x))))))/(x^2 +x)) ] = − [((4(√(x^2 +x))−(((2x+1)^2 )/( (√(x^2 +x)))))/(x^2 +x)) ] = − [ ((4x^2 +4x−4x^2 −4x−1)/((x^2 +x)(√(x^2 +x)))) ] = (1/(x(x+1)(√(x^2 +x)))) correct sir Liberty.](Q122226.png)
Answered by TANMAY PANACEA last updated on 14/Nov/20

| ||
Question and Answers Forum | ||
Question Number 122205 by mathmax by abdo last updated on 14/Nov/20 | ||
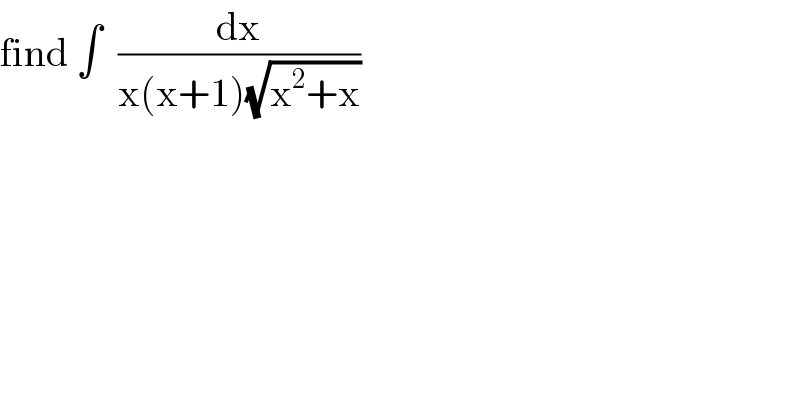 | ||
Commented by liberty last updated on 15/Nov/20 | ||
![∫ (dx/((x^2 +x)^(3/2) )) = ∫ (dx/(x^3 (1+x^(−1) )^(3/2) )) = ∫ ((x^(−2) dx)/(x(1+x^(−1) )^(3/2) )) ; [ u^(2/3) = 1+(1/x) ] ⇒ [ (2/3)u^(−(1/3)) du = −x^(−2) dx ] J = ∫ (u^(2/3) −1)(−(2/3)u^(−(1/3)) du)((1/u)) J= −(2/3)∫ (u^(2/3) −1)(u^(−(4/3)) ) du J=−(2/3)∫ (u^(−(2/3)) −u^(−(4/3)) ) du J = −(2/3)[ 3u^(1/3) +3u^(−(1/3)) ] + c J = −2(√((x+1)/x))−2(√(x/(x+1))) + c J= −2(((x+1+x)/( (√(x^2 +x)))))+ c = −((4x+2)/( (√(x^2 +x)))) + c](Q122225.png) | ||
Commented by benjo_mathlover last updated on 15/Nov/20 | ||
![let J(x)=−((4x+2)/( (√(x^2 +x)))) ((dJ(x))/dx) = − [ ((4(√(x^2 +x))−(4x+2)(((2x+1)/(2(√(x^2 +x))))))/(x^2 +x)) ] = − [((4(√(x^2 +x))−(((2x+1)^2 )/( (√(x^2 +x)))))/(x^2 +x)) ] = − [ ((4x^2 +4x−4x^2 −4x−1)/((x^2 +x)(√(x^2 +x)))) ] = (1/(x(x+1)(√(x^2 +x)))) correct sir Liberty.](Q122226.png) | ||
Answered by TANMAY PANACEA last updated on 14/Nov/20 | ||
 | ||
| ||