Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 12228 by tawa last updated on 16/Apr/17

Solve the differential equation (dy/dx) = ((2xy)/(x^2 + y^2 ))

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{2xy}}{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} } \\ $$

Answered by mrW1 last updated on 16/Apr/17

u=(y/x) y=ux (dy/dx)=x(du/dx)+u (dy/dx)=((2xy)/(x^2 +y^2 ))⇒ x(du/dx)+u=((2u)/(1+u^2 )) x(du/dx)=((2u)/(1+u^2 ))−u=((u(1−u^2 ))/(1+u^2 )) ((1+u^2 )/(u(1−u^2 )))du=(1/x)dx ∫((1+u^2 )/(u(1−u^2 )))du=∫(1/x)dx (1/2)∫((1+u^2 )/(u^2 (1−u^2 )))du^2 =∫(1/x)dx (1/2)∫((1+w)/(w(1−w)))dw=∫(1/x)dx (w=u^2 ) ∫[(1/w)+(2/(1−w))]du=2∫(1/x)dx ln w−2ln (1−w)=2ln x+C_1 ln (w/(x^2 (1−w)^2 ))=C_1 ln (u^2 /(x^2 (1−u^2 )^2 ))=C_1 2ln (u/(x(1−u^2 )))=C_1 (u/(x(1−u^2 )))=e^(C_1 /2) =(1/C) (y/(x^2 (1−(y^2 /x^2 ))))=(1/C) (y/(x^2 −y^2 ))=(1/C) y^2 +Cy=x^2

$${u}=\frac{{y}}{{x}} \\ $$$${y}={ux} \\ $$$$\frac{{dy}}{{dx}}={x}\frac{{du}}{{dx}}+{u} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\Rightarrow \\ $$$${x}\frac{{du}}{{dx}}+{u}=\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$${x}\frac{{du}}{{dx}}=\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }−{u}=\frac{{u}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}+{u}^{\mathrm{2}} }{{u}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{du}=\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\int\frac{\mathrm{1}+{u}^{\mathrm{2}} }{{u}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{du}=\int\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+{u}^{\mathrm{2}} }{{u}^{\mathrm{2}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)}{du}^{\mathrm{2}} =\int\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+{w}}{{w}\left(\mathrm{1}−{w}\right)}{dw}=\int\frac{\mathrm{1}}{{x}}{dx}\:\:\:\:\:\:\:\left({w}={u}^{\mathrm{2}} \right) \\ $$$$\int\left[\frac{\mathrm{1}}{{w}}+\frac{\mathrm{2}}{\mathrm{1}−{w}}\right]{du}=\mathrm{2}\int\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\mathrm{ln}\:{w}−\mathrm{2ln}\:\left(\mathrm{1}−{w}\right)=\mathrm{2ln}\:{x}+{C}_{\mathrm{1}} \\ $$$$\mathrm{ln}\:\frac{{w}}{{x}^{\mathrm{2}} \left(\mathrm{1}−{w}\right)^{\mathrm{2}} }={C}_{\mathrm{1}} \\ $$$$\mathrm{ln}\:\frac{{u}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} }={C}_{\mathrm{1}} \\ $$$$\mathrm{2ln}\:\frac{{u}}{{x}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}={C}_{\mathrm{1}} \\ $$$$\frac{{u}}{{x}\left(\mathrm{1}−{u}^{\mathrm{2}} \right)}={e}^{\frac{{C}_{\mathrm{1}} }{\mathrm{2}}} =\frac{\mathrm{1}}{{C}} \\ $$$$\frac{{y}}{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}=\frac{\mathrm{1}}{{C}} \\ $$$$\frac{{y}}{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }=\frac{\mathrm{1}}{{C}} \\ $$$${y}^{\mathrm{2}} +{Cy}={x}^{\mathrm{2}} \\ $$

Commented by tawa last updated on 16/Apr/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by ajfour last updated on 16/Apr/17

error in line 6.

$${error}\:{in}\:{line}\:\mathrm{6}. \\ $$

Commented by mrW1 last updated on 16/Apr/17

you are right.

$${you}\:{are}\:{right}. \\ $$

Commented by tawa last updated on 16/Apr/17

please sir, mrw the cubic root equation formular.. i need the image again sir

$$\mathrm{please}\:\mathrm{sir},\:\mathrm{mrw}\:\mathrm{the}\:\mathrm{cubic}\:\mathrm{root}\:\mathrm{equation}\:\mathrm{formular}..\:\mathrm{i}\:\mathrm{need}\:\mathrm{the}\:\mathrm{image}\:\mathrm{again}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 16/Apr/17

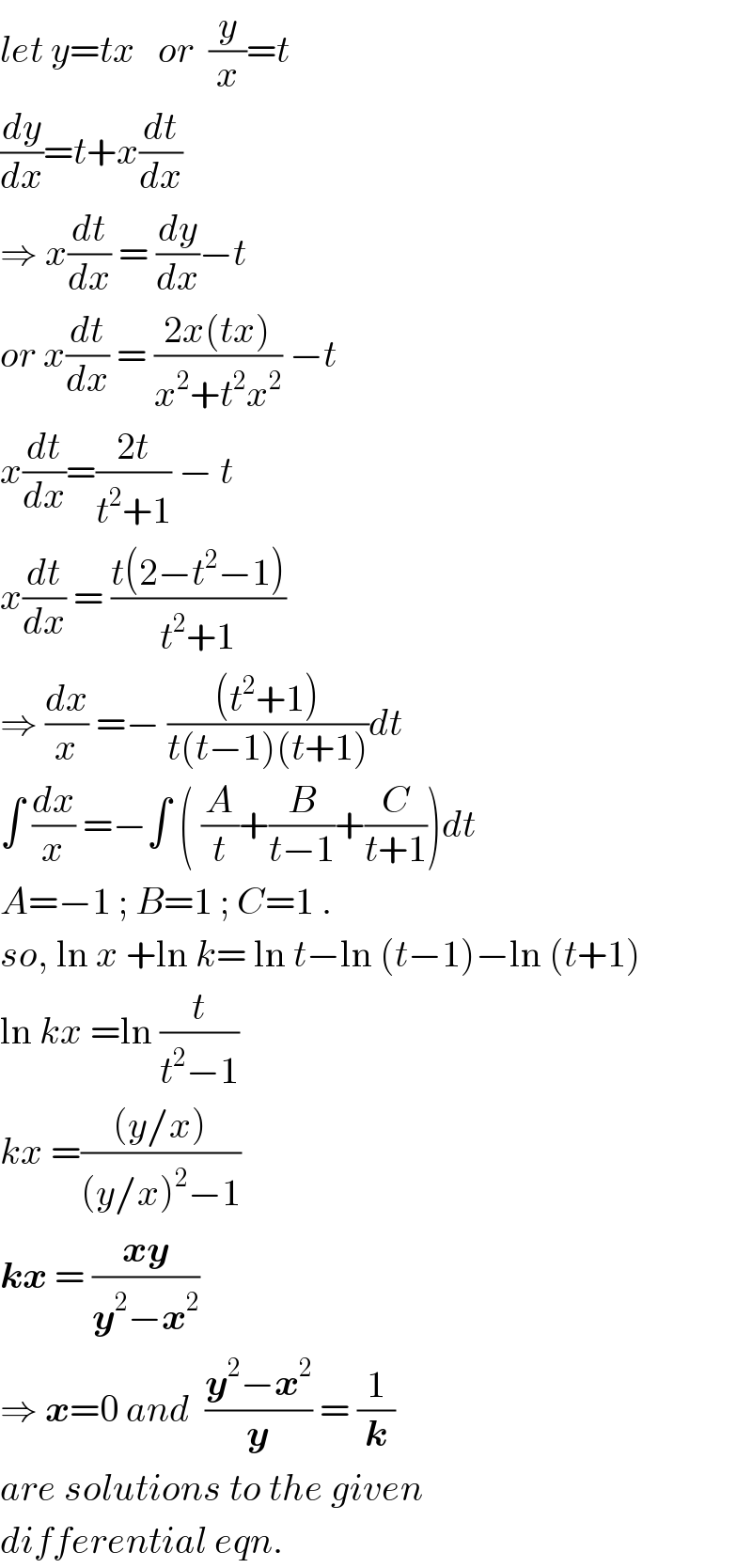
let y=tx or (y/x)=t (dy/dx)=t+x(dt/dx) ⇒ x(dt/dx) = (dy/dx)−t or x(dt/dx) = ((2x(tx))/(x^2 +t^2 x^2 )) −t x(dt/dx)=((2t)/(t^2 +1)) − t x(dt/dx) = ((t(2−t^2 −1))/(t^2 +1)) ⇒ (dx/x) =− (((t^2 +1))/(t(t−1)(t+1)))dt ∫ (dx/x) =−∫ ( (A/t)+(B/(t−1))+(C/(t+1)))dt A=−1 ; B=1 ; C=1 . so, ln x +ln k= ln t−ln (t−1)−ln (t+1) ln kx =ln (t/(t^2 −1)) kx =(((y/x))/((y/x)^2 −1)) kx = ((xy)/(y^2 −x^2 )) ⇒ x=0 and ((y^2 −x^2 )/y) = (1/k) are solutions to the given differential eqn.

$${let}\:{y}={tx}\:\:\:{or}\:\:\frac{{y}}{{x}}={t} \\ $$$$\frac{{dy}}{{dx}}={t}+{x}\frac{{dt}}{{dx}} \\ $$$$\Rightarrow\:{x}\frac{{dt}}{{dx}}\:=\:\frac{{dy}}{{dx}}−{t} \\ $$$${or}\:{x}\frac{{dt}}{{dx}}\:=\:\frac{\mathrm{2}{x}\left({tx}\right)}{{x}^{\mathrm{2}} +{t}^{\mathrm{2}} {x}^{\mathrm{2}} }\:−{t} \\ $$$${x}\frac{{dt}}{{dx}}=\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\:−\:{t} \\ $$$${x}\frac{{dt}}{{dx}}\:=\:\frac{{t}\left(\mathrm{2}−{t}^{\mathrm{2}} −\mathrm{1}\right)}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\:\frac{{dx}}{{x}}\:=−\:\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{dt} \\ $$$$\int\:\frac{{dx}}{{x}}\:=−\int\:\left(\:\frac{{A}}{{t}}+\frac{{B}}{{t}−\mathrm{1}}+\frac{{C}}{{t}+\mathrm{1}}\right){dt} \\ $$$${A}=−\mathrm{1}\:;\:{B}=\mathrm{1}\:;\:{C}=\mathrm{1}\:. \\ $$$${so},\:\mathrm{ln}\:{x}\:+\mathrm{ln}\:{k}=\:\mathrm{ln}\:{t}−\mathrm{ln}\:\left({t}−\mathrm{1}\right)−\mathrm{ln}\:\left({t}+\mathrm{1}\right) \\ $$$$\mathrm{ln}\:{kx}\:=\mathrm{ln}\:\frac{{t}}{{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$${kx}\:=\frac{\left({y}/{x}\right)}{\left({y}/{x}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\boldsymbol{{kx}}\:=\:\frac{\boldsymbol{{xy}}}{\boldsymbol{{y}}^{\mathrm{2}} −\boldsymbol{{x}}^{\mathrm{2}} }\:\: \\ $$$$\Rightarrow\:\boldsymbol{{x}}=\mathrm{0}\:{and}\:\:\frac{\boldsymbol{{y}}^{\mathrm{2}} −\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{y}}}\:=\:\frac{\mathrm{1}}{\boldsymbol{{k}}}\: \\ $$$${are}\:{solutions}\:{to}\:{the}\:{given} \\ $$$${differential}\:{eqn}. \\ $$

Commented by tawa last updated on 16/Apr/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com