
Question and Answers Forum
Question Number 122293 by mathocean1 last updated on 15/Nov/20
![given f(x)=cos^2 x for x ∈ [−(π/(12));(π/(12 ))] , ∣f′(x)∣≤(1/2). 1) show that ∀ x, y ∈ [−(π/(12));(π/(12))] ; ∣cos^2 x−cos^2 y∣≤(1/2)∣x−y∣](Q122293.png)
Commented by ZiYangLee last updated on 16/Nov/20
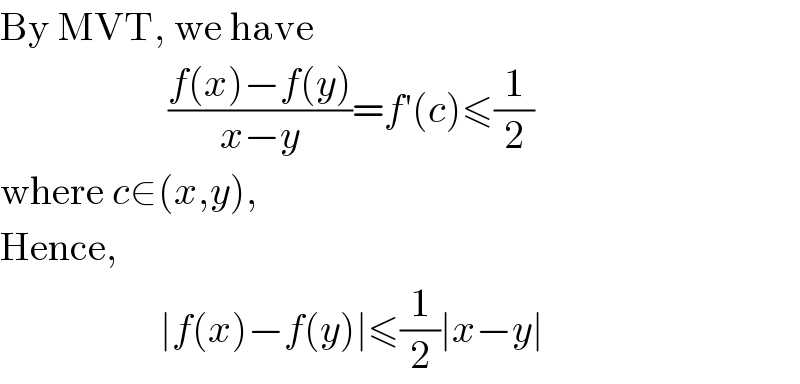
Answered by mathmax by abdo last updated on 15/Nov/20
![∀x ∈[−(π/(12)),(π/(12))] ∣f^′ (x)∣≤(1/2) ⇒−(1/2)≤f^′ (x)≤(1/2) ⇒ −(1/2)∫_x ^y dt ≤∫_x ^y f^′ (t)dt ≤(1/2)∫_x ^y dt ⇒ −(1/2)(y−x) ≤f(y)−f(x)≤(1/2)(y−x) ⇒∣f(x)−f(y)∣≤(1/2)∣x−y∣ ⇒ ∣cos^2 x−cos^2 y∣≤((∣x−y∣)/2)](Q122332.png)
| ||
Question and Answers Forum | ||
Question Number 122293 by mathocean1 last updated on 15/Nov/20 | ||
![given f(x)=cos^2 x for x ∈ [−(π/(12));(π/(12 ))] , ∣f′(x)∣≤(1/2). 1) show that ∀ x, y ∈ [−(π/(12));(π/(12))] ; ∣cos^2 x−cos^2 y∣≤(1/2)∣x−y∣](Q122293.png) | ||
Commented by ZiYangLee last updated on 16/Nov/20 | ||
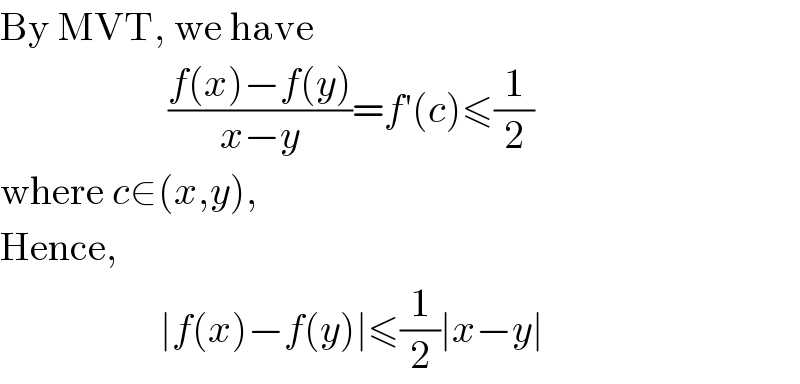 | ||
Answered by mathmax by abdo last updated on 15/Nov/20 | ||
![∀x ∈[−(π/(12)),(π/(12))] ∣f^′ (x)∣≤(1/2) ⇒−(1/2)≤f^′ (x)≤(1/2) ⇒ −(1/2)∫_x ^y dt ≤∫_x ^y f^′ (t)dt ≤(1/2)∫_x ^y dt ⇒ −(1/2)(y−x) ≤f(y)−f(x)≤(1/2)(y−x) ⇒∣f(x)−f(y)∣≤(1/2)∣x−y∣ ⇒ ∣cos^2 x−cos^2 y∣≤((∣x−y∣)/2)](Q122332.png) | ||
| ||