Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 122322 by EngLewis last updated on 15/Nov/20

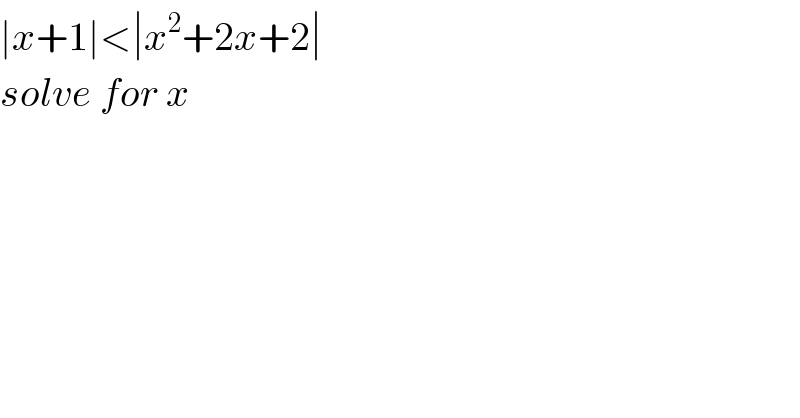
∣x+1∣<∣x^2 +2x+2∣ solve for x

$$\mid{x}+\mathrm{1}\mid<\mid{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\mid \\ $$ $${solve}\:{for}\:{x} \\ $$

Answered by mathmax by abdo last updated on 15/Nov/20

we have x^2 +2x+2 =(x+1)^2 +1>0 ⇒∣x^2 +2x+2∣=x^2 +2x+2 e⇒∣x+1∣−x^2 −2x−2<0 let f(x)=∣x+1∣−x^2 −2x−2 x −∞ −1 +∞ ∣x+1∣ −x−1 0 x+1 f(x) −x^2 −3x−3 −x^2 −x−1 ⇒ f(x)= { ((−x^2 −3x−3 ,x≤−1)),((−x^2 −x−1 ,x≥−1)) :} case1 x≤−1 f(x)<0 ⇒−x^2 −3x−3<0 ⇒x^2 +3x+3>0 Δ=9−12 =−3 ⇒this polynom is slways >0 ⇒S_1 =]−∞ ,−1] case2 x≥1 f(x)<0 ⇒−x^2 −x−1<0 ⇒x^2 +x+1>0 this polynom is also >0 ⇒S_2 =[−1,+∞[ so S =∪ S_i =R

$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\:=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}>\mathrm{0}\:\Rightarrow\mid\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\mid=\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2} \\ $$ $$\mathrm{e}\Rightarrow\mid\mathrm{x}+\mathrm{1}\mid−\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{2}<\mathrm{0}\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mid\mathrm{x}+\mathrm{1}\mid−\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{2} \\ $$ $$\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$ $$\mid\mathrm{x}+\mathrm{1}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{x}+\mathrm{1} \\ $$ $$\mathrm{f}\left(\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{3}\:\:\:\:\:\:\:\:\:\:−\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\: \\ $$ $$\Rightarrow\:\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{−\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{3}\:\:,\mathrm{x}\leqslant−\mathrm{1}}\\{−\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}\:,\mathrm{x}\geqslant−\mathrm{1}}\end{cases} \\ $$ $$\mathrm{case1}\:\:\mathrm{x}\leqslant−\mathrm{1}\:\:\:\mathrm{f}\left(\mathrm{x}\right)<\mathrm{0}\:\Rightarrow−\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{3}<\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{3}>\mathrm{0} \\ $$ $$\left.\Delta\left.=\mathrm{9}−\mathrm{12}\:=−\mathrm{3}\:\Rightarrow\mathrm{this}\:\mathrm{polynom}\:\mathrm{is}\:\mathrm{slways}\:>\mathrm{0}\:\Rightarrow\mathrm{S}_{\mathrm{1}} =\right]−\infty\:,−\mathrm{1}\right] \\ $$ $$\mathrm{case2}\:\:\mathrm{x}\geqslant\mathrm{1}\:\:\mathrm{f}\left(\mathrm{x}\right)<\mathrm{0}\:\Rightarrow−\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{1}<\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}>\mathrm{0} \\ $$ $$\mathrm{this}\:\mathrm{polynom}\:\mathrm{is}\:\mathrm{also}\:>\mathrm{0}\:\Rightarrow\mathrm{S}_{\mathrm{2}} =\left[−\mathrm{1},+\infty\left[\:\:\mathrm{so}\right.\right. \\ $$ $$\mathrm{S}\:=\cup\:\mathrm{S}_{\mathrm{i}} =\mathrm{R}\: \\ $$

Answered by MJS_new last updated on 15/Nov/20

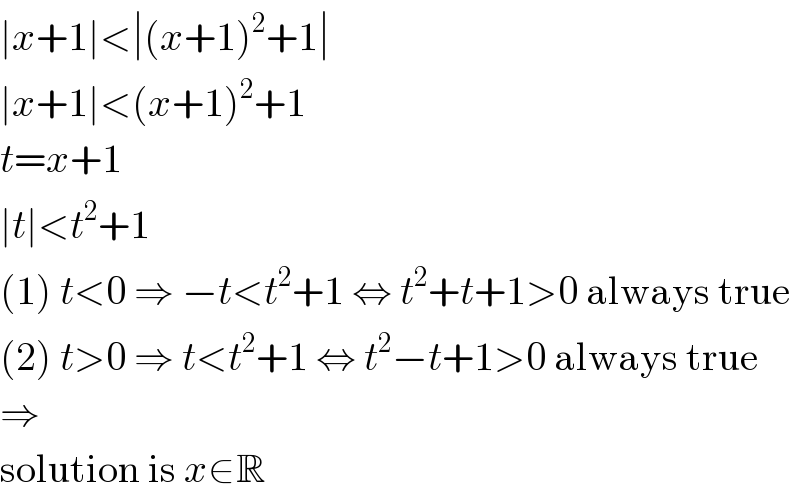
∣x+1∣<∣(x+1)^2 +1∣ ∣x+1∣<(x+1)^2 +1 t=x+1 ∣t∣<t^2 +1 (1) t<0 ⇒ −t<t^2 +1 ⇔ t^2 +t+1>0 always true (2) t>0 ⇒ t<t^2 +1 ⇔ t^2 −t+1>0 always true ⇒ solution is x∈R

$$\mid{x}+\mathrm{1}\mid<\mid\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\mid \\ $$ $$\mid{x}+\mathrm{1}\mid<\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1} \\ $$ $${t}={x}+\mathrm{1} \\ $$ $$\mid{t}\mid<{t}^{\mathrm{2}} +\mathrm{1} \\ $$ $$\left(\mathrm{1}\right)\:{t}<\mathrm{0}\:\Rightarrow\:−{t}<{t}^{\mathrm{2}} +\mathrm{1}\:\Leftrightarrow\:{t}^{\mathrm{2}} +{t}+\mathrm{1}>\mathrm{0}\:\mathrm{always}\:\mathrm{true} \\ $$ $$\left(\mathrm{2}\right)\:{t}>\mathrm{0}\:\Rightarrow\:{t}<{t}^{\mathrm{2}} +\mathrm{1}\:\Leftrightarrow\:{t}^{\mathrm{2}} −{t}+\mathrm{1}>\mathrm{0}\:\mathrm{always}\:\mathrm{true} \\ $$ $$\Rightarrow \\ $$ $$\mathrm{solution}\:\mathrm{is}\:{x}\in\mathbb{R} \\ $$

Answered by mathmax by abdo last updated on 15/Nov/20

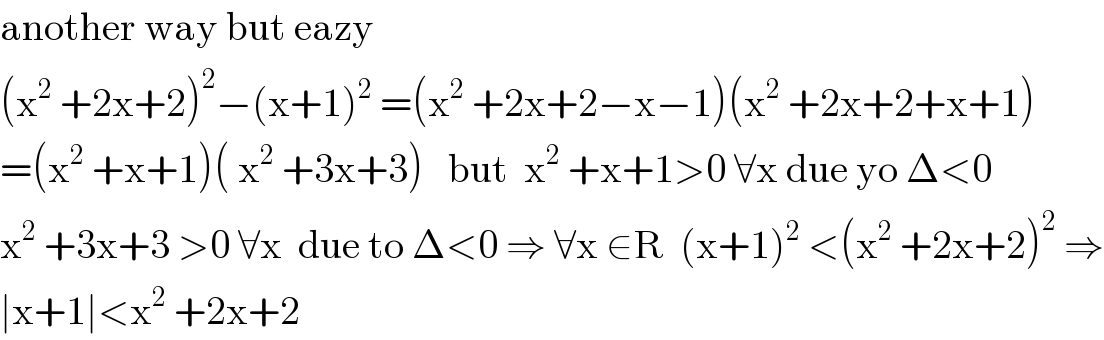
another way but eazy (x^2 +2x+2)^2 −(x+1)^2 =(x^2 +2x+2−x−1)(x^2 +2x+2+x+1) =(x^2 +x+1)( x^2 +3x+3) but x^2 +x+1>0 ∀x due yo Δ<0 x^2 +3x+3 >0 ∀x due to Δ<0 ⇒ ∀x ∈R (x+1)^2 <(x^2 +2x+2)^2 ⇒ ∣x+1∣<x^2 +2x+2

$$\mathrm{another}\:\mathrm{way}\:\mathrm{but}\:\mathrm{eazy} \\ $$ $$\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} −\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:=\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}−\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}+\mathrm{x}+\mathrm{1}\right) \\ $$ $$=\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)\left(\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{3}\right)\:\:\:\mathrm{but}\:\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}>\mathrm{0}\:\forall\mathrm{x}\:\mathrm{due}\:\mathrm{yo}\:\Delta<\mathrm{0} \\ $$ $$\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}+\mathrm{3}\:>\mathrm{0}\:\forall\mathrm{x}\:\:\mathrm{due}\:\mathrm{to}\:\Delta<\mathrm{0}\:\Rightarrow\:\forall\mathrm{x}\:\in\mathrm{R}\:\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:<\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}\right)^{\mathrm{2}} \:\Rightarrow \\ $$ $$\mid\mathrm{x}+\mathrm{1}\mid<\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2} \\ $$

Answered by TANMAY PANACEA last updated on 16/Nov/20

x^2 +2x+2 (x+1)^2 +1 (x+1)^2 always positive so (x+1)^2 +1 always greater than (x+1)

$${x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2} \\ $$ $$\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1} \\ $$ $$\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:{always}\:{positive} \\ $$ $${so}\:\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\:{always}\:{greater}\:{than}\:\left({x}+\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com