Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 122329 by mathocean1 last updated on 15/Nov/20

find n ∈ N such that 5^(2n) +5^n ≡0[13]

$${find}\:{n}\:\in\:\mathbb{N}\:{such}\:{that} \\ $$$$\mathrm{5}^{\mathrm{2}{n}} +\mathrm{5}^{{n}} \equiv\mathrm{0}\left[\mathrm{13}\right] \\ $$

Answered by 676597498 last updated on 15/Nov/20

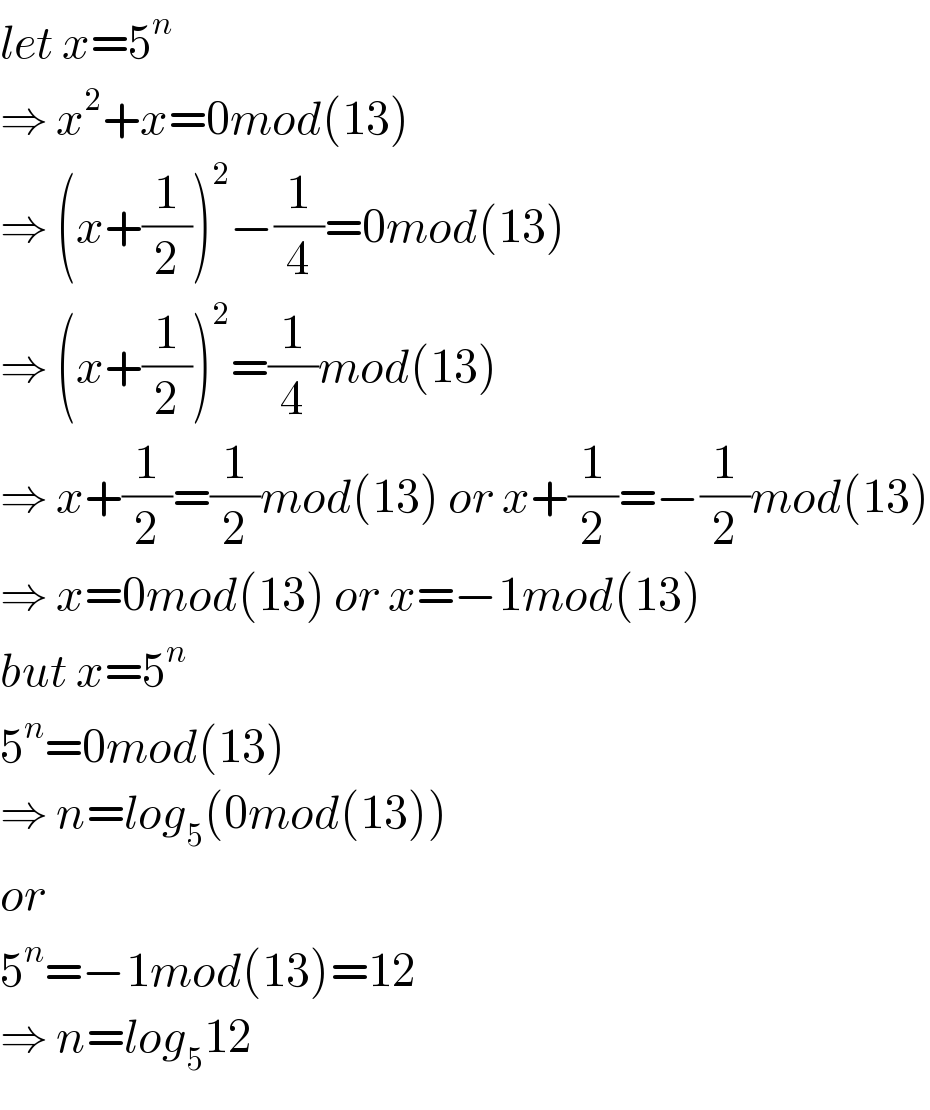
let x=5^n ⇒ x^2 +x=0mod(13) ⇒ (x+(1/2))^2 −(1/4)=0mod(13) ⇒ (x+(1/2))^2 =(1/4)mod(13) ⇒ x+(1/2)=(1/2)mod(13) or x+(1/2)=−(1/2)mod(13) ⇒ x=0mod(13) or x=−1mod(13) but x=5^n 5^n =0mod(13) ⇒ n=log_5 (0mod(13)) or 5^n =−1mod(13)=12 ⇒ n=log_5 12

$${let}\:{x}=\mathrm{5}^{{n}} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} +{x}=\mathrm{0}{mod}\left(\mathrm{13}\right) \\ $$$$\Rightarrow\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0}{mod}\left(\mathrm{13}\right) \\ $$$$\Rightarrow\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}{mod}\left(\mathrm{13}\right) \\ $$$$\Rightarrow\:{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}{mod}\left(\mathrm{13}\right)\:{or}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{2}}{mod}\left(\mathrm{13}\right) \\ $$$$\Rightarrow\:{x}=\mathrm{0}{mod}\left(\mathrm{13}\right)\:{or}\:{x}=−\mathrm{1}{mod}\left(\mathrm{13}\right) \\ $$$${but}\:{x}=\mathrm{5}^{{n}} \\ $$$$\mathrm{5}^{{n}} =\mathrm{0}{mod}\left(\mathrm{13}\right) \\ $$$$\Rightarrow\:{n}={log}_{\mathrm{5}} \left(\mathrm{0}{mod}\left(\mathrm{13}\right)\right) \\ $$$${or}\: \\ $$$$\mathrm{5}^{{n}} =−\mathrm{1}{mod}\left(\mathrm{13}\right)=\mathrm{12} \\ $$$$\Rightarrow\:{n}={log}_{\mathrm{5}} \mathrm{12} \\ $$

Commented by mindispower last updated on 16/Nov/20

x∈N

$${x}\in\mathbb{N} \\ $$

Answered by MJS_new last updated on 15/Nov/20

5^(2n) +5^n =13m; m∈N 5^n (5^n +1)=13m 5^n ≠13m [obviously] ⇒ 5^n =13m−1 trying the first few n we get n=4k+2

$$\mathrm{5}^{\mathrm{2}{n}} +\mathrm{5}^{{n}} =\mathrm{13}{m};\:{m}\in\mathbb{N} \\ $$$$\mathrm{5}^{{n}} \left(\mathrm{5}^{{n}} +\mathrm{1}\right)=\mathrm{13}{m} \\ $$$$\mathrm{5}^{{n}} \neq\mathrm{13}{m}\:\left[\mathrm{obviously}\right] \\ $$$$\Rightarrow\:\mathrm{5}^{{n}} =\mathrm{13}{m}−\mathrm{1} \\ $$$$\mathrm{trying}\:\mathrm{the}\:\mathrm{first}\:\mathrm{few}\:{n}\:\mathrm{we}\:\mathrm{get} \\ $$$${n}=\mathrm{4}{k}+\mathrm{2} \\ $$

Answered by floor(10²Eta[1]) last updated on 16/Nov/20

5^n (5^n +1)≡0(mod13) 5^n ≡0(mod13) ∨ 5^n ≡12(mod 13) ⇒5^n ≡12(mod13) n=2⇒5^n =5^2 ≡12(mod13) 5^(n−2) ≡1(mod13) 5^a ≡1(mod13)⇒a∣ϕ(13)=12⇒a=4∴a=4k ⇒n−2=4k⇒n=4k+2, ∀ k≥0

$$\mathrm{5}^{\mathrm{n}} \left(\mathrm{5}^{\mathrm{n}} +\mathrm{1}\right)\equiv\mathrm{0}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{5}^{\mathrm{n}} \equiv\mathrm{0}\left(\mathrm{mod13}\right)\:\vee\:\mathrm{5}^{\mathrm{n}} \equiv\mathrm{12}\left(\mathrm{mod}\:\mathrm{13}\right) \\ $$$$\Rightarrow\mathrm{5}^{\mathrm{n}} \equiv\mathrm{12}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{n}=\mathrm{2}\Rightarrow\mathrm{5}^{\mathrm{n}} =\mathrm{5}^{\mathrm{2}} \equiv\mathrm{12}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{5}^{\mathrm{n}−\mathrm{2}} \equiv\mathrm{1}\left(\mathrm{mod13}\right) \\ $$$$\mathrm{5}^{\mathrm{a}} \equiv\mathrm{1}\left(\mathrm{mod13}\right)\Rightarrow\mathrm{a}\mid\varphi\left(\mathrm{13}\right)=\mathrm{12}\Rightarrow\mathrm{a}=\mathrm{4}\therefore\mathrm{a}=\mathrm{4k} \\ $$$$\Rightarrow\mathrm{n}−\mathrm{2}=\mathrm{4k}\Rightarrow\mathrm{n}=\mathrm{4k}+\mathrm{2},\:\forall\:\mathrm{k}\geqslant\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com