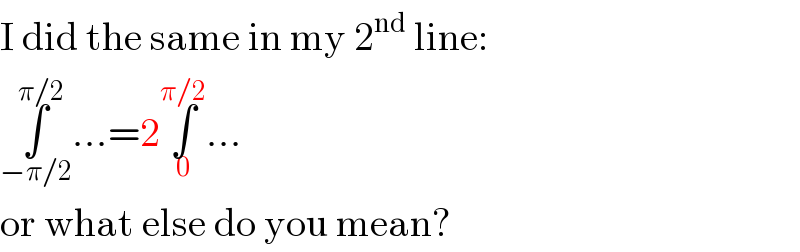Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 122496 by benjo_mathlover last updated on 17/Nov/20

$$V=\underset{0}{\stackrel{3}{\int }}\frac{xdx}{\sqrt{x+1}+\sqrt{5x+1}}$$$$T=\underset{-\pi /2}{\stackrel{\pi /2}{\int }}\sqrt{\cos x-\cos {}^{3}x}dx$$

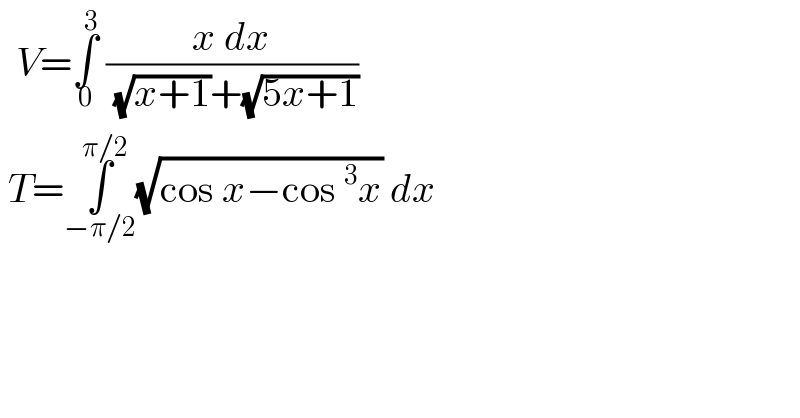
Answered by Dwaipayan Shikari last updated on 17/Nov/20

$${\int }_0^3\frac{x}{\sqrt{x+1}+\sqrt{5x+1}}dx={\int }_0^3\frac{\sqrt{5x+1}-\sqrt{x+1}}{4}dx$$$$=\frac{1}{30}{(5x+1)}^{\frac{3}{2}}-\frac{1}{6}{(x+1)}^{\frac{3}{2}}=\frac{1}{30}{\left(16\right)}^{\frac{3}{2}}-\frac{1}{6}{4}^{\frac{3}{2}}-\frac{1}{30}+\frac{1}{6}$$$$=\frac{63}{30}-\frac{7}{6}=\frac{63}{30}-\frac{35}{30}=\frac{14}{15}$$

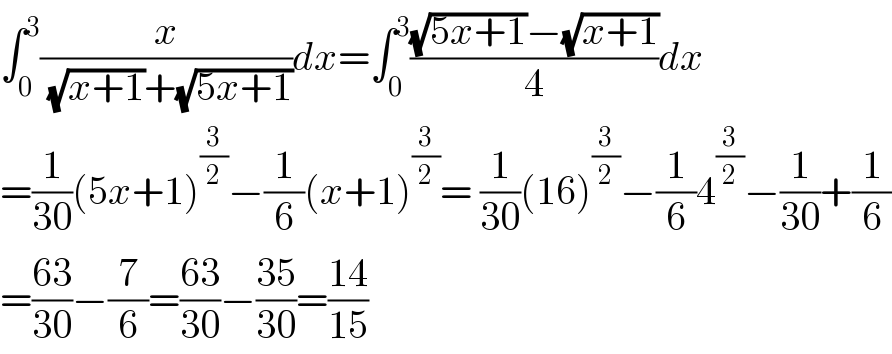
Answered by MJS_new last updated on 17/Nov/20

$$\underset{-\pi /2}{\stackrel{\pi /2}{\int }}\sqrt{\cos x-{\cos }^{3}x}dx=\underset{-\pi /2}{\stackrel{\pi /2}{\int }}\sqrt{(1-{\cos }^{2}x)\cos x}dx=$$$$=\underset{-\pi /2}{\stackrel{\pi /2}{\int }}\mid \sin x\mid \sqrt{\cos x}dx=2\underset{0}{\stackrel{\pi /2}{\int }}\sin x\sqrt{\cos x}dx=$$$$[t=\cos x\to dx=-\frac{dt}{\sin x}]$$$$=-2\underset{1}{\stackrel{0}{\int }}\sqrt{t}dt=2\underset{0}{\stackrel{1}{\int }}\sqrt{t}dt=2{\left[\frac{2}{3}{t}^{3/2}\right]}_0^1=\frac{4}{3}$$

Commented by liberty last updated on 17/Nov/20

$$\mathrm{on}\mathrm{interval}-\frac{\pi }{2}⩽\mathrm{x}⩽0\Rightarrow \mid \sin \mathrm{x}\mid =-\sin \mathrm{x}\mathrm{sir}?$$$$\mathrm{it}\mathrm{should}\mathrm{be}\underset{-\pi /2}{\stackrel{0}{\int }}-\sin \mathrm{x}\sqrt{\cos \mathrm{x}}\mathrm{dx}+\underset{0}{\stackrel{\pi /2}{\int }}\sin \mathrm{x}\sqrt{\cos \mathrm{x}}\mathrm{dx}$$$$\mathrm{let}\cos \mathrm{x}=\mathrm{u}\to \{\begin{array}{l}\mathrm{u}=1\\ \mathrm{u}=0\end{array}$$$$\underset{0}{\stackrel{1}{\int }}\sqrt{\mathrm{u}}\mathrm{du}-\underset{1}{\stackrel{0}{\int }}\sqrt{\mathrm{u}}\mathrm{du}=2{\int }_0^1\sqrt{\mathrm{u}}\mathrm{du}$$$$={\left[\frac{4}{3}{\mathrm{u}}^{3/2}\right]}_0^1=\frac{4}{3}.$$

Commented by MJS_new last updated on 17/Nov/20

$$\mathrm{I}\mathrm{did}\mathrm{the}\mathrm{same}\mathrm{in}\mathrm{my}{2}^{\mathrm{nd}}\mathrm{line}:$$$$\underset{-\pi /2}{\stackrel{\pi /2}{\int }}...=2\underset{0}{\stackrel{\pi /2}{\int }}...$$$$\mathrm{or}\mathrm{what}\mathrm{else}\mathrm{do}\mathrm{you}\mathrm{mean}?$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com