Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 122528 by mnjuly1970 last updated on 17/Nov/20

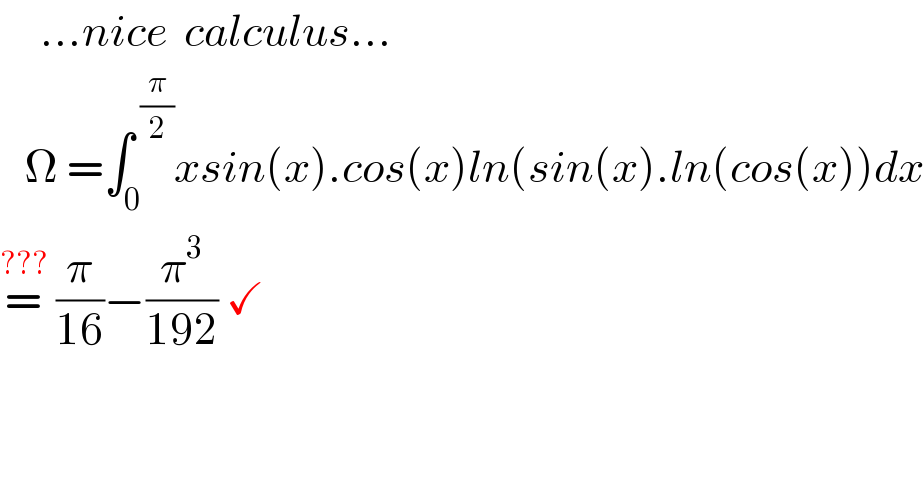
...nice calculus... Ω =∫_0 ^( (π/2)) xsin(x).cos(x)ln(sin(x).ln(cos(x))dx =^(???) (π/(16))−(π^3 /(192)) ✓

$$\:\:\:\:\:...{nice}\:\:{calculus}... \\ $$$$\:\:\:\Omega\:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {xsin}\left({x}\right).{cos}\left({x}\right){ln}\left({sin}\left({x}\right).{ln}\left({cos}\left({x}\right)\right){dx}\right. \\ $$$$\overset{???} {=}\:\frac{\pi}{\mathrm{16}}−\frac{\pi^{\mathrm{3}} }{\mathrm{192}}\:\checkmark \\ $$

Answered by mindispower last updated on 18/Nov/20

∫_a ^b f(x)dx=(1/2)∫_a ^b (f(a+b−x)+f(x))dx ⇔=(1/2)∫_0 ^(π/2) .(π/2)sin(x)cos(x)ln(sin(x))ln(cos(x))dx Ω=(π/4)∫_0 ^(π/2) sin(x)cos(x)ln(sin(x))ln(cos(x))dx f(a,b)=(π/4)∫_0 ^(π/2) sin(x)cos(x)sin^a (x)cos^b (x)dx Ω=(∂^2 /(∂a∂b))f(0,0) f=(π/8).2∫_0 ^(π/2) sin^(2(1+(a/2))−1) (x).cos^(2(1+(b/2))−1) (x)dx =(π/8)β(1+a,1+b) (∂/∂b)((∂/∂a))f=(π/8).(∂/∂b).(1/2)β((a/2)+1,(b/2)+1)(Ψ((a/2)+1)−Ψ((1/2)(a+b)+2) =(π/(32))β((a/2)+1,(b/2)+1)(Ψ((b/2)+1)−Ψ((1/2)(a+b)+2))(Ψ((a/2)+1)−Ψ((1/2)(a+b)+2)) −(π/(32))Ψ^1 ((1/2)(a+b)+2)β((a/2)+1,(b/2)+1) Ω=(π/(32))β(1,1)(Ψ(1)−Ψ(2))^2 −(π/(32))Ψ^1 (2)β(1,1) =(π/(32))−(π/(32))Ψ′(2) Ψ^1 (z)=Σ_(n≥0) (1/((n+z)^2 )) Ψ^1 (2)=Σ_(n≥0) (1/((n+2)^2 ))=Σ_(n≥1) ((1/n^2 ))−1=(π^2 /6)−1 =(π/(32))−(π/(32))((π^2 /6)−1) =(𝛑/(16))−(π^3 /(192))

$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{{a}} ^{{b}} \left({f}\left({a}+{b}−{x}\right)+{f}\left({x}\right)\right){dx} \\ $$$$\Leftrightarrow=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} .\frac{\pi}{\mathrm{2}}{sin}\left({x}\right){cos}\left({x}\right){ln}\left({sin}\left({x}\right)\right){ln}\left({cos}\left({x}\right)\right){dx} \\ $$$$\Omega=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}\left({x}\right){cos}\left({x}\right){ln}\left({sin}\left({x}\right)\right){ln}\left({cos}\left({x}\right)\right){dx} \\ $$$${f}\left({a},{b}\right)=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}\left({x}\right){cos}\left({x}\right){sin}^{{a}} \left({x}\right){cos}^{{b}} \left({x}\right){dx} \\ $$$$\Omega=\frac{\partial^{\mathrm{2}} }{\partial{a}\partial{b}}{f}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${f}=\frac{\pi}{\mathrm{8}}.\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}\left(\mathrm{1}+\frac{{a}}{\mathrm{2}}\right)−\mathrm{1}} \left({x}\right).{cos}^{\mathrm{2}\left(\mathrm{1}+\frac{{b}}{\mathrm{2}}\right)−\mathrm{1}} \left({x}\right){dx} \\ $$$$=\frac{\pi}{\mathrm{8}}\beta\left(\mathrm{1}+{a},\mathrm{1}+{b}\right) \\ $$$$\frac{\partial}{\partial{b}}\left(\frac{\partial}{\partial{a}}\right){f}=\frac{\pi}{\mathrm{8}}.\frac{\partial}{\partial{b}}.\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{{a}}{\mathrm{2}}+\mathrm{1},\frac{{b}}{\mathrm{2}}+\mathrm{1}\right)\left(\Psi\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{b}\right)+\mathrm{2}\right)\right. \\ $$$$=\frac{\pi}{\mathrm{32}}\beta\left(\frac{{a}}{\mathrm{2}}+\mathrm{1},\frac{{b}}{\mathrm{2}}+\mathrm{1}\right)\left(\Psi\left(\frac{{b}}{\mathrm{2}}+\mathrm{1}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{b}\right)+\mathrm{2}\right)\right)\left(\Psi\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{b}\right)+\mathrm{2}\right)\right) \\ $$$$−\frac{\pi}{\mathrm{32}}\Psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{b}\right)+\mathrm{2}\right)\beta\left(\frac{{a}}{\mathrm{2}}+\mathrm{1},\frac{{b}}{\mathrm{2}}+\mathrm{1}\right) \\ $$$$\Omega=\frac{\pi}{\mathrm{32}}\beta\left(\mathrm{1},\mathrm{1}\right)\left(\Psi\left(\mathrm{1}\right)−\Psi\left(\mathrm{2}\right)\right)^{\mathrm{2}} −\frac{\pi}{\mathrm{32}}\Psi^{\mathrm{1}} \left(\mathrm{2}\right)\beta\left(\mathrm{1},\mathrm{1}\right) \\ $$$$=\frac{\pi}{\mathrm{32}}−\frac{\pi}{\mathrm{32}}\Psi'\left(\mathrm{2}\right) \\ $$$$\Psi^{\mathrm{1}} \left({z}\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+{z}\right)^{\mathrm{2}} } \\ $$$$\Psi^{\mathrm{1}} \left(\mathrm{2}\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)^{\mathrm{2}} }=\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)−\mathrm{1}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$$$=\frac{\pi}{\mathrm{32}}−\frac{\pi}{\mathrm{32}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}\right) \\ $$$$=\frac{\boldsymbol{\pi}}{\mathrm{16}}−\frac{\pi^{\mathrm{3}} }{\mathrm{192}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 18/Nov/20

thank you sir power ... by using the euler beta function .grateful .sincerely yours.m.n

$${thank}\:{you}\:{sir}\:{power}\:... \\ $$$$\:{by}\:{using}\:{the}\:{euler}\:{beta}\:{function} \\ $$$$.{grateful}\:.{sincerely}\:{yours}.{m}.{n} \\ $$

Commented by mindispower last updated on 18/Nov/20

withe pleasur nice day

$${withe}\:{pleasur}\:{nice}\:{day} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com