
Question and Answers Forum
Question Number 122588 by bramlexs22 last updated on 18/Nov/20
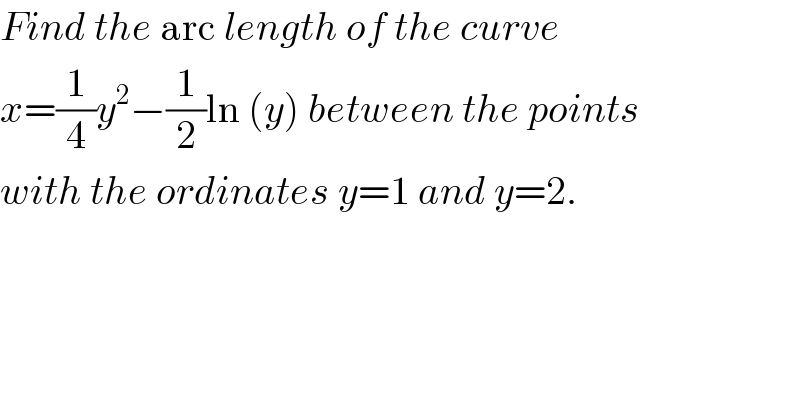
Answered by MJS_new last updated on 18/Nov/20
![arc length of x=f(y) is given by ∫(√(1+(x′)^2 )) dy x=(1/4)y^2 −(1/2)ln y is defined for y>0 x′=(y/2)−(1/(2y)) (√(1+(x′)^2 ))=(√(((y^2 +1)^2 )/(4y^2 )))=((y^2 +1)/(2y)) [because y>0] ∫((y^2 +1)/(2y))dy=∫(y/2)+(1/(2y))dy=(1/4)y^2 +(1/2)ln y ⇒ arc length is (3/4)+(1/2)ln 2](Q122590.png)
Commented by bramlexs22 last updated on 18/Nov/20
Answered by liberty last updated on 18/Nov/20
![ℓ = ∫_1 ^2 (√(1+(x′)^2 )) dy (dx/dy) = (1/2)y−(1/(2y)) ⇒ℓ=∫_1 ^2 (√(1+((1/2)y−(1/(2y)))^2 )) dy ℓ = ∫_1 ^2 (√(1+(1/4)y^2 +(1/(4y^2 ))−(1/2))) dy ℓ = ∫_1 ^2 (√((1/4)y^2 +(1/2)+(1/(4y^2 )))) dy ℓ = ∫_1 ^2 ((1/2)y+(1/(2y))) dy = [(1/4)y^2 +((ln y)/2) ]_1 ^2 ℓ = (3/4)+((ln 2)/2). ▲](Q122591.png)
| ||
Question and Answers Forum | ||
Question Number 122588 by bramlexs22 last updated on 18/Nov/20 | ||
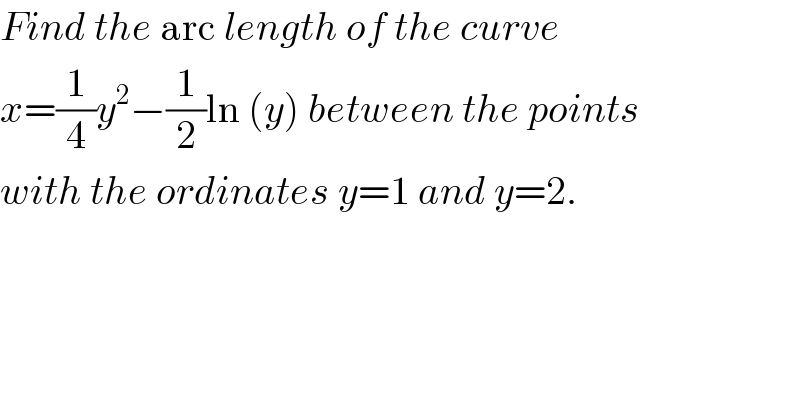 | ||
Answered by MJS_new last updated on 18/Nov/20 | ||
![arc length of x=f(y) is given by ∫(√(1+(x′)^2 )) dy x=(1/4)y^2 −(1/2)ln y is defined for y>0 x′=(y/2)−(1/(2y)) (√(1+(x′)^2 ))=(√(((y^2 +1)^2 )/(4y^2 )))=((y^2 +1)/(2y)) [because y>0] ∫((y^2 +1)/(2y))dy=∫(y/2)+(1/(2y))dy=(1/4)y^2 +(1/2)ln y ⇒ arc length is (3/4)+(1/2)ln 2](Q122590.png) | ||
| ||
Commented by bramlexs22 last updated on 18/Nov/20 | ||
 | ||
Answered by liberty last updated on 18/Nov/20 | ||
![ℓ = ∫_1 ^2 (√(1+(x′)^2 )) dy (dx/dy) = (1/2)y−(1/(2y)) ⇒ℓ=∫_1 ^2 (√(1+((1/2)y−(1/(2y)))^2 )) dy ℓ = ∫_1 ^2 (√(1+(1/4)y^2 +(1/(4y^2 ))−(1/2))) dy ℓ = ∫_1 ^2 (√((1/4)y^2 +(1/2)+(1/(4y^2 )))) dy ℓ = ∫_1 ^2 ((1/2)y+(1/(2y))) dy = [(1/4)y^2 +((ln y)/2) ]_1 ^2 ℓ = (3/4)+((ln 2)/2). ▲](Q122591.png) | ||
| ||