
Question and Answers Forum
Question Number 122631 by MJS_new last updated on 18/Nov/20
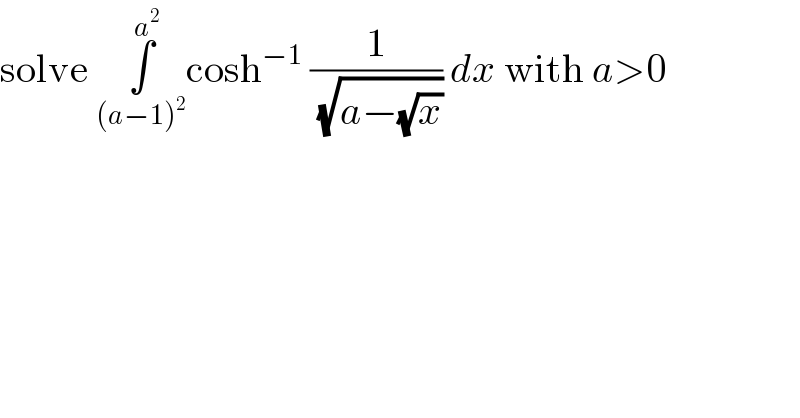
Commented byliberty last updated on 18/Nov/20
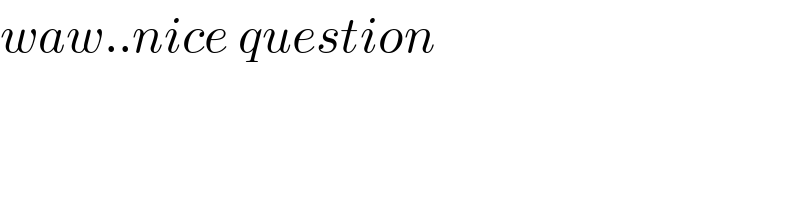
Commented byMJS_new last updated on 19/Nov/20
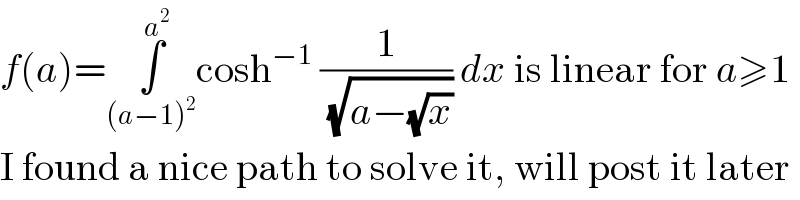
Answered by mathmax by abdo last updated on 18/Nov/20

Commented byMJS_new last updated on 19/Nov/20

Answered by MJS_new last updated on 19/Nov/20
![∫cosh^(−1) (1/( (√(a−(√x))))) dx= by parts but with a simple trick: u^′ =1 → u=x−a^2 v=cosh^(−1) (1/( (√(a−(√x))))) → v′=−(1/(4(√x)((√x)−a)(√((√x)−a+1)))) =(x−a^2 )cosh^(−1) (1/( (√(a−(√x)))))+(1/4)∫((x−a^2 )/( (√x)((√x)−a)(√((√x)−a+1))))dx= (1/4)∫((x−a^2 )/( (√x)((√x)−a)(√((√x)−a+1))))dx= [t=(√((√x)−a+1)) → dx=4(√x)(√((√x)−a+1))dt] =∫(t^2 +2a−1)dt=(1/3)t(t^2 +3(2a−1))= =(1/3)((√x)+5a−2)(√((√x)−a+1)) =(x−a^2 )cosh^(−1) (1/( (√(a−(√x))))) +(1/3)((√x)+5a−2)(√((√x)−a+1))+C inserting the borders we get f(a)=(2a−1)cosh^(−1) (1/( (√(a−∣a−1∣)))) −(((5a+∣a−1∣−2)(√(1−a+∣a−1∣)))/3)+(((5a+∣a∣−2)(√(1−a+∣a∣)))/3) for 0<a<1 we get f(a)=(2a−1)cosh^(−1) (1/( (√(2a−1)))) −(((4a−1)(√(2(1−a))))/3)+((2(3a−1))/3) for a≥1 we get f(a)=((2(3a−1))/3)](Q122747.png)
Commented byliberty last updated on 19/Nov/20
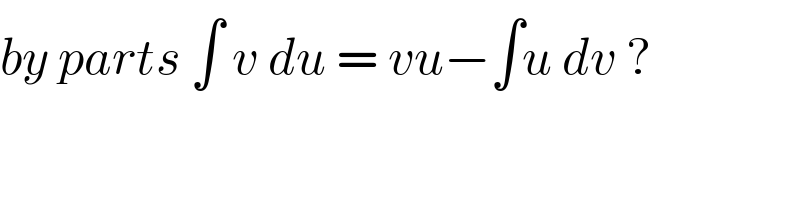
Commented byMJS_new last updated on 19/Nov/20

Commented byliberty last updated on 19/Nov/20
Commented byMJS_new last updated on 19/Nov/20

