
Question and Answers Forum
Question Number 122689 by john santu last updated on 19/Nov/20

Answered by bobhans last updated on 19/Nov/20
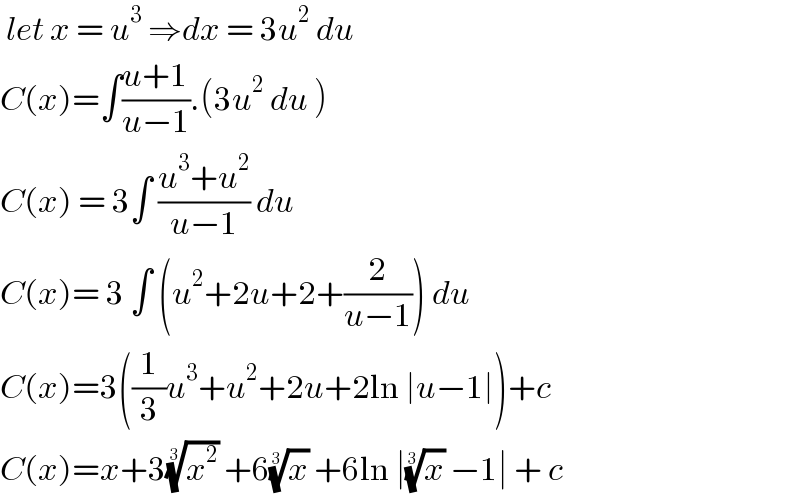
Commented by MJS_new last updated on 19/Nov/20
![another possibility: ∫((x^(1/3) +1)/(x^(1/3) −1))dx=∫dx+∫(2/(x^(1/3) −1))dx [t=x^(1/3) −1 → dx=3x^(2/3) dt] =x+6∫(((t+1)^2 )/t)dt=x+3t(t+4)+6ln t = =x+3(x^(1/3) −1)(x^(1/3) +3)+6ln ∣x^(1/3) −1∣ +C](Q122693.png)
Commented by john santu last updated on 19/Nov/20

| ||
Question and Answers Forum | ||
Question Number 122689 by john santu last updated on 19/Nov/20 | ||
 | ||
Answered by bobhans last updated on 19/Nov/20 | ||
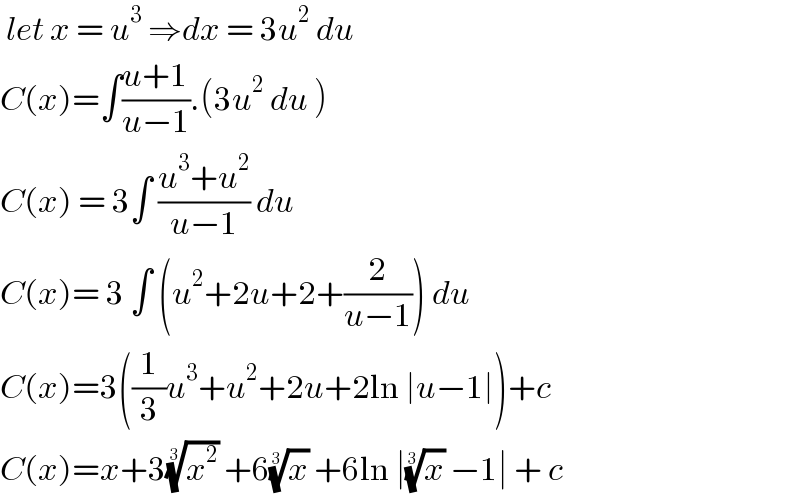 | ||
| ||
Commented by MJS_new last updated on 19/Nov/20 | ||
![another possibility: ∫((x^(1/3) +1)/(x^(1/3) −1))dx=∫dx+∫(2/(x^(1/3) −1))dx [t=x^(1/3) −1 → dx=3x^(2/3) dt] =x+6∫(((t+1)^2 )/t)dt=x+3t(t+4)+6ln t = =x+3(x^(1/3) −1)(x^(1/3) +3)+6ln ∣x^(1/3) −1∣ +C](Q122693.png) | ||
Commented by john santu last updated on 19/Nov/20 | ||
 | ||