
Question and Answers Forum
Question Number 122704 by mnjuly1970 last updated on 19/Nov/20
![... general calculus... i: (1/( (√(1−4x)))) =^(??) Σ_(n=0 ) ^∞ [ (((2n)),(( n)) ) x^n ] ii: (π/2) =^? Σ_(n=0) ^∞ [( (((2n)),(( n)) )/4^n ) (1/((2n+1)))]](Q122704.png)
Answered by Dwaipayan Shikari last updated on 19/Nov/20
![(1/( (√(1−4x)))) =(1−4x)^(−(1/2)) =1+2x+(3/4)16x^2 +((15)/8)64x^3 +... = 1+2x+12x^2 +120x^3 +.. = 1+((2!)/(1!))x+((4!)/(2!))x^2 +((6!)/(3!))x^3 +..=Σ_(n=0) ^∞ [ (((2n)),(n) )x^n ]](Q122706.png)
Answered by Dwaipayan Shikari last updated on 19/Nov/20
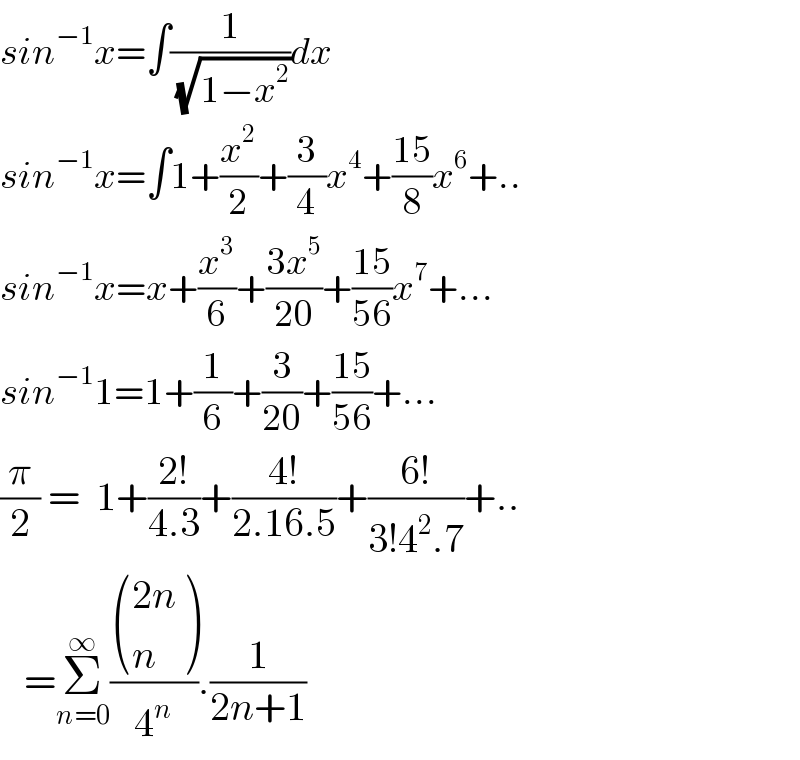
Commented by mnjuly1970 last updated on 19/Nov/20
Commented by Dwaipayan Shikari last updated on 19/Nov/20

Answered by mnjuly1970 last updated on 19/Nov/20
![solution ii in (i): 4x=t^2 (1/( (√(1−t^2 ))))=Σ_(n=0) ^∞ [ (((2n)),(( n)) ) (t^(2n) /4^n )] ∫_0 ^( x) (1/( (√(1−t^2 ))))dt=Σ_(n≥0) { (((2n)),(( n)) ) [(t^(2n+1) /((2n+1)4^n ))]_0 ^x } Arcsin(x)=Σ_(n=0) ^∞ (((2n)),(( n)) ) (x^(2n+1) /((2n+1)4^n )) x=1 :: (π/2) =Σ[ (((2n)),(( n)) ) (1/((2n+1)4^n )) ] ✓](Q122710.png)
