Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 122739 by mohammad17 last updated on 19/Nov/20

$$1){\int }_{-\pi }^{\pi }\frac{dx}{{sin}^{2}x+1}$$$$$$$$2){\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{x^2}{x^4+5x^2+4}dx$$

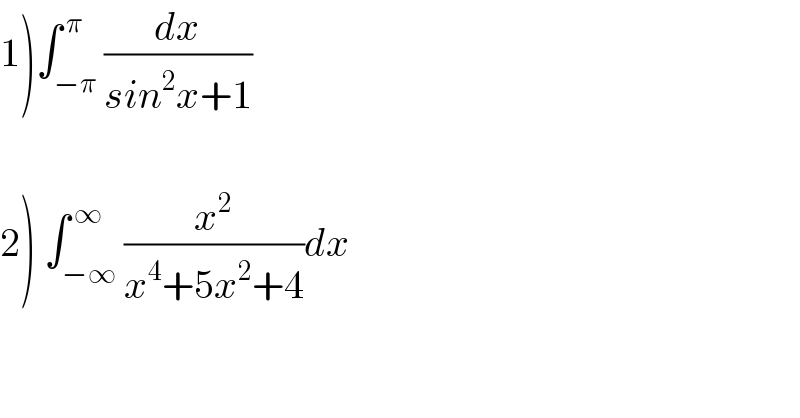
Answered by Dwaipayan Shikari last updated on 19/Nov/20

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{x^2}{(x^4+5x^2+4)}dx$$$$={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{x^2}{(x^2+4)(x^2+1)}dx$$$$=-\frac{1}{3}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{x^2+1}-\frac{4}{x^2+4}=-\frac{1}{3}(\pi -2\pi )=\frac{\pi }{3}$$

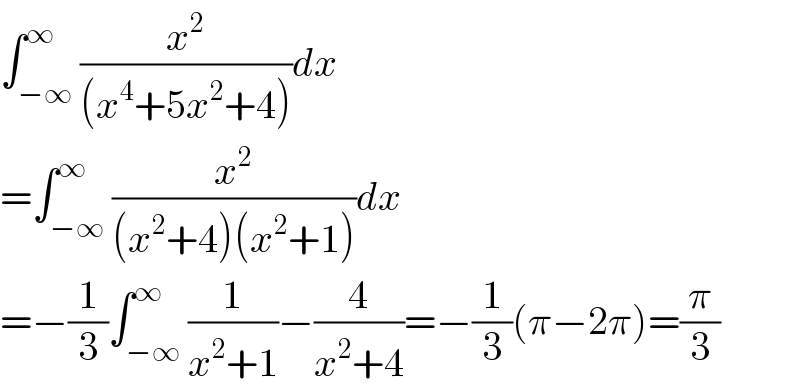
Commented by mohammad17 last updated on 19/Nov/20

$$thankyoumis$$

Answered by MJS_new last updated on 19/Nov/20

$$\int \frac{dx}{1+{\sin }^{2}x}=$$$$[t=\tan x\to dx=\frac{dt}{t^2+1}]$$$$=\int \frac{dt}{2t^2+1}=\frac{\sqrt{2}}{2}\arctan \left(\sqrt{2}t\right)=$$$$=\frac{\sqrt{2}}{2}\arctan \left(\sqrt{2}\tan x\right)+C$$$$\underset{-\pi }{\stackrel{\pi }{\int }}\frac{dx}{1+{\sin }^{2}x}=4\underset{0}{\stackrel{\pi /2}{\int }}\frac{dx}{1+{\sin }^{2}x}$$$$\Rightarrow \mathrm{answer}\mathrm{is}\pi \sqrt{2}$$

Commented by mohammad17 last updated on 19/Nov/20

$$putsiranswer\sqrt{2\pi }$$

Commented by MJS_new last updated on 19/Nov/20

$$\mathrm{sorry}{\mathrm{you}}^{\prime }\mathrm{re}\mathrm{right},\mathrm{I}\mathrm{corrected}\mathrm{my}\mathrm{result}$$

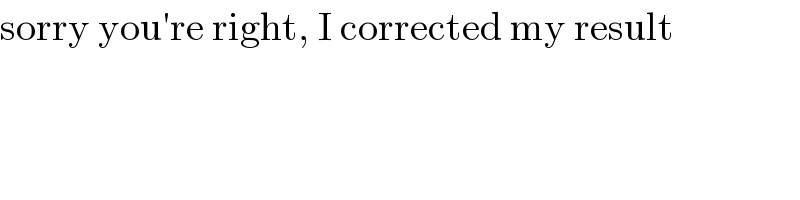
Commented by mohammad17 last updated on 19/Nov/20

$$nowitsright$$

Answered by bemath last updated on 19/Nov/20

$$\left(1\right)let\tan \left(\frac{x}{2}\right)=v\Rightarrow dx=2\cos {}^2\left(\frac{x}{2}\right)dv$$$$so\int \frac{2}{1+v^2}.\frac{{(1+v^2)}^2}{v^4+6v^2+1}dv$$$$\int \frac{2(1+v^2)}{v^4+6v^2+9-8}dv=\int \frac{2(1+v^2)}{{(v^2+3)}^2-8}dv$$$$\int \frac{2(1+v^2)}{(v^2+3-\sqrt{8})(v^2+3+\sqrt{8})}dv$$$$continue..$$

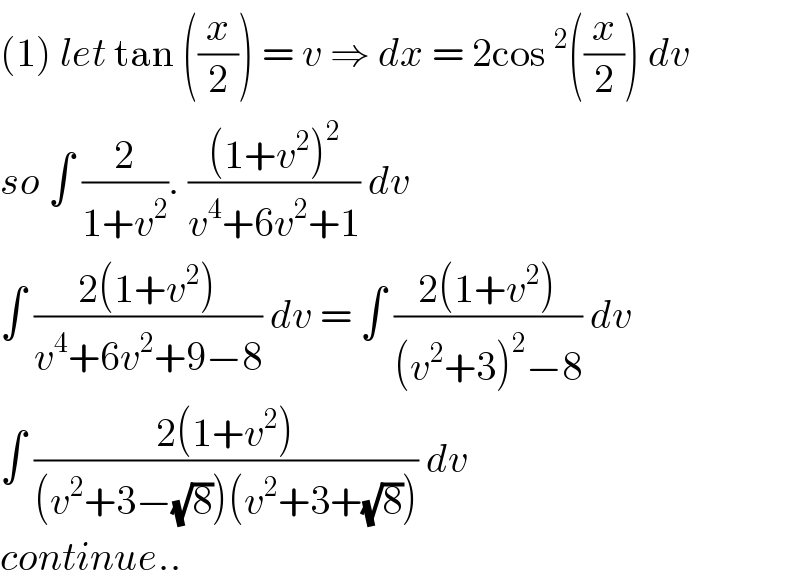
Answered by Bird last updated on 19/Nov/20

$$1)I={\int }_{-\pi }^{\pi }\frac{dx}{{sin}^{2}x+1}\Rightarrow$$$$I={\int }_{-\pi }^{\pi }\frac{dx}{\frac{1-cos\left(2x\right)}{2}+1}$$$$={\int }_{-\pi }^{\pi }\frac{2dx}{3-cos\left(2x\right)}$$$${=}_{2x=t}{\int }_{-2\pi }^{2\pi }\frac{dt}{3-cost}$$$$=2{\int }_0^{2\pi }\frac{dt}{3-cost}$$$${=}_{z=e^{it}}2{\int }_{\mid z\mid =1}\frac{dz}{iz(3-\frac{z+z^{-1}}{2})}$$$$=-4i{\int }_{\mid z\mid =1}\frac{dz}{z(6-z-z^{-1})}$$$$=-4i{\int }_{\mid z\mid =1}\frac{dz}{6z-z^2-1}$$$$={\int }_{\mid z\mid =1}\frac{4idz}{z^2-6z+1}$$$$\phi \left(z\right)=\frac{4i}{z^2-6z+1}$$$${\mathrm{\Delta }}^{{}^{\prime }}=9-1=8\Rightarrow z_1=3+2\sqrt{2}$$$${\mathrm{z}}_2=3-2\sqrt{2}$$$$\phi \left(z\right)=\frac{4i}{(z-z_1)(z-z_2)}$$$$\mid z_1\mid -1=3+2\sqrt{2}-1=2+2\sqrt{2}>0$$$$\mid z_2\mid -1=3-2\sqrt{2}-1=2-2\sqrt{2}<0$$$$\Rightarrow {\int }_{\mid z\mid =1}\phi \left(z\right)dz=2i\pi Res(\phi ,z_2)$$$$=2i\pi \times \frac{4i}{(z_2-z_1)}=\frac{-8\pi }{-4\sqrt{2}}=\frac{2\pi }{\sqrt{2}}$$$$=\frac{2\pi \sqrt{2}}{2}=\pi \sqrt{2}\Rightarrow I=\pi \sqrt{2}$$

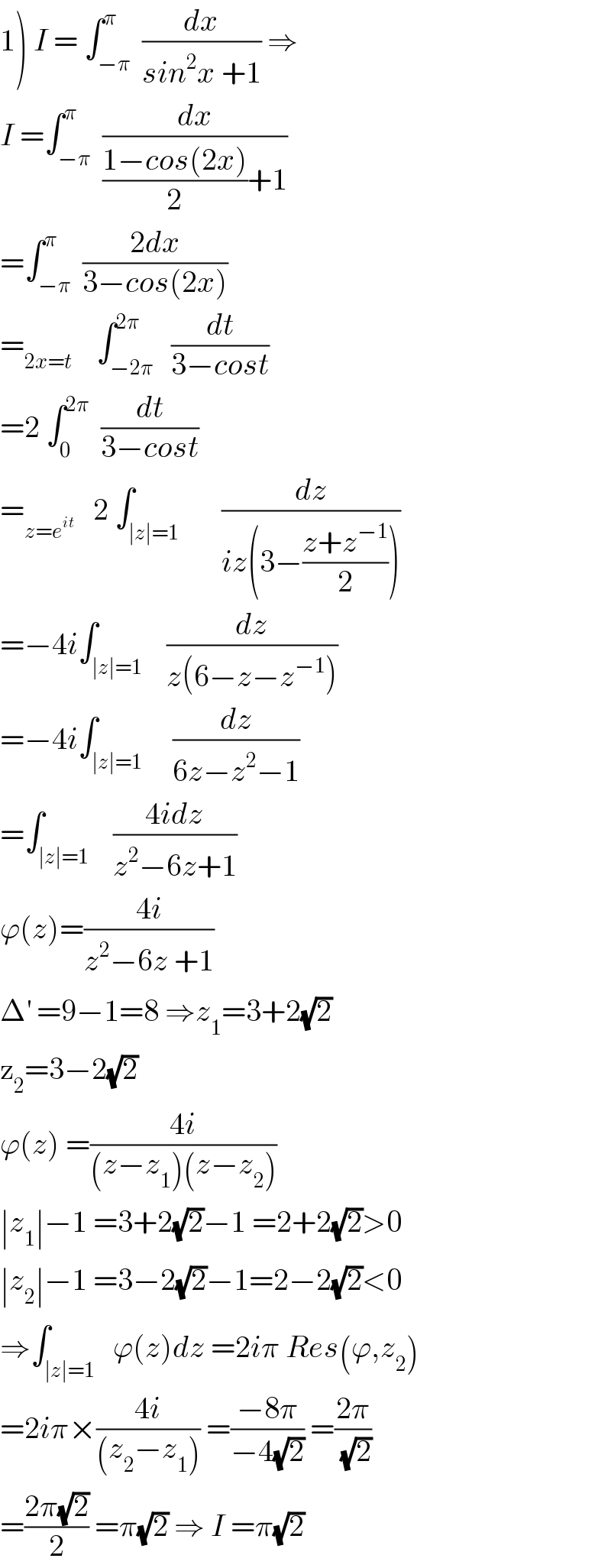
Answered by mathmax by abdo last updated on 20/Nov/20

$$2)\mathrm{A}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{{\mathrm{x}}^2}{{\mathrm{x}}^4+{5\mathrm{x}}^2+4}\mathrm{dx}\mathrm{let}\mathrm{decompose}\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{u}}{{\mathrm{u}}^2+5\mathrm{u}+4}$$$$\mathrm{\Delta }=25-16=9\Rightarrow {\mathrm{u}}_1=\frac{-5+3}{2}=-1\mathrm{and}{\mathrm{u}}_2=\frac{-5-3}{2}=-4\Rightarrow$$$$\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{u}}{(\mathrm{u}+1)(\mathrm{u}+4)}=\frac{1}{3}\mathrm{u}(\frac{1}{\mathrm{u}+1}-\frac{1}{\mathrm{u}+4})=\frac{1}{3}(\frac{\mathrm{u}}{\mathrm{u}+1}-\frac{\mathrm{u}}{\mathrm{u}+4})$$$$=\frac{1}{3}(\frac{\mathrm{u}+1-1}{\mathrm{u}+1}-\frac{\mathrm{u}+4-4}{\mathrm{u}+4})=\frac{1}{3}(1-\frac{1}{\mathrm{u}+1}-1+\frac{4}{\mathrm{u}+4})=\frac{1}{3}(\frac{4}{\mathrm{u}+4}-\frac{1}{\mathrm{u}+1})$$$$\Rightarrow \mathrm{A}=\frac{1}{3}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\{\frac{4}{{\mathrm{x}}^2+4}-\frac{1}{{\mathrm{x}}^2+1}\}\mathrm{dx}$$$$=\frac{4}{3}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{dx}}{{\mathrm{x}}^2+4}-\frac{1}{3}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{dx}}{{\mathrm{x}}^2+1}\mathrm{dx}\mathrm{we}\mathrm{have}$$$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{dx}}{{\mathrm{x}}^2+4}=2\mathrm{i}\pi \mathrm{Res}(\mathrm{f},2\mathrm{i})=2\mathrm{i}\pi \times \frac{1}{4\mathrm{i}}=\frac{\pi }{2}$$$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{\mathrm{dx}}{{\mathrm{x}}^2+1}\mathrm{dx}=2\mathrm{i}\pi \mathrm{Res}(\mathrm{f},\mathrm{i})=2\mathrm{i}\pi .\frac{1}{2\mathrm{i}}=\pi \Rightarrow$$$$\mathrm{A}=\frac{4}{3}.\frac{\pi }{2}-\frac{\pi }{3}=\frac{2\pi }{3}-\frac{\pi }{3}\Rightarrow \mathrm{A}=\frac{\pi }{3}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com