
Question Number 12279 by chux last updated on 17/Apr/17
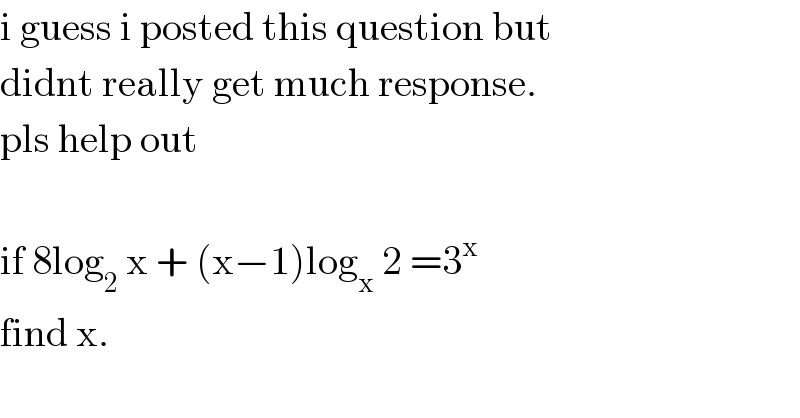
$$\mathrm{i}\:\mathrm{guess}\:\mathrm{i}\:\mathrm{posted}\:\mathrm{this}\:\mathrm{question}\:\mathrm{but} \\ $$$$\mathrm{didnt}\:\mathrm{really}\:\mathrm{get}\:\mathrm{much}\:\mathrm{response}. \\ $$$$\mathrm{pls}\:\mathrm{help}\:\mathrm{out} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{8log}_{\mathrm{2}} \:\mathrm{x}\:+\:\left(\mathrm{x}−\mathrm{1}\right)\mathrm{log}_{\mathrm{x}} \:\mathrm{2}\:=\mathrm{3}^{\mathrm{x}} \: \\ $$$$\mathrm{find}\:\mathrm{x}. \\ $$
Commented by mrW1 last updated on 17/Apr/17

$${there}\:{is}\:{no}\:{analytical}\:{solution}\:{for} \\ $$$${such}\:{equation}.\:{by}\:{trial}\:{and}\:{error}\:{you} \\ $$$${can}\:{see}\:{that}\:{x}=\mathrm{2}\:{is}\:{a}\:{solution}.\:{using} \\ $$$${graphical}\:{method}\:{you}\:{can}\:{find}\:{the} \\ $$$${other}\:{solution}\:{x}\approx\mathrm{1}.\mathrm{3853}. \\ $$
Commented by mrW1 last updated on 18/Apr/17

$${the}\:\mathrm{newton}\:\mathrm{raphson}\:\mathrm{iteration}\:{to}\:{solve} \\ $$$${f}\left({x}\right)=\mathrm{0}\:{is}: \\ $$$${if}\:{you}\:{have}\:{a}\:{start}\:{value}\:{x}_{\mathrm{0}} \:{for}\:{the}\:{solution}, \\ $$$${you}\:{can}\:{get}\:{a}\:{better}\:{value}\:{with} \\ $$$${x}_{{n}+\mathrm{1}} ={x}_{{n}} −\frac{{f}\left({x}_{{n}} \right)}{{f}'\left({x}_{{n}} \right)}\:\:\:\:\:\left({n}=\mathrm{1},\mathrm{2},\mathrm{3}....\right) \\ $$$${you}\:{repeat}\:{this}\:{till}\:{x}_{{n}+\mathrm{1}} −{x}_{{n}} \:{is}\:{small} \\ $$$${enough}\:{for}\:{you}. \\ $$$$ \\ $$$${your}\:{case}\:{is}\:{not}\:{good}\:{for}\:{demonstration}. \\ $$$${let}\:{us}\:{see}\:{f}\left({x}\right)=\mathrm{sin}\:{x}−\mathrm{0}.\mathrm{4}=\mathrm{0} \\ $$$${f}'\left({x}\right)=\mathrm{cos}\:{x} \\ $$$${x}_{\mathrm{0}} =\mathrm{0}.\mathrm{4} \\ $$$${x}_{\mathrm{1}} =\mathrm{0}.\mathrm{4}−\frac{\mathrm{sin}\:\mathrm{0}.\mathrm{4}−\mathrm{0}.\mathrm{4}}{\mathrm{cos}\:\mathrm{0}.\mathrm{4}}=\mathrm{0}.\mathrm{411488553} \\ $$$${x}_{\mathrm{2}} =\mathrm{0}.\mathrm{411488553}−\frac{\mathrm{sin}\:\mathrm{0}.\mathrm{411488553}−\mathrm{0}.\mathrm{4}}{\mathrm{cos}\:\mathrm{0}.\mathrm{411488553}}=\mathrm{0}.\mathrm{411516846} \\ $$$${x}_{\mathrm{3}} =....=\mathrm{0}.\mathrm{411516846}\approx{x}_{\mathrm{2}} \\ $$$${we}\:{get}\:{after}\:\mathrm{3}\:{iterations}\:{a}\:{good}\:{solution} \\ $$$${for}\:\mathrm{sin}\:{x}−\mathrm{0}.\mathrm{4}=\mathrm{0}:\: \\ $$$${x}\approx\mathrm{0}.\mathrm{411516846} \\ $$
Commented by chux last updated on 18/Apr/17

$$\mathrm{thanks}\:\mathrm{sir}.....\:\mathrm{a}\:\mathrm{friend}\:\mathrm{told}\:\mathrm{me}\:\mathrm{about} \\ $$$$\mathrm{a}\:\mathrm{method}\:\mathrm{called}\:\mathrm{newton}\:\mathrm{raphson} \\ $$$$\mathrm{iteration}\:\mathrm{but}\:\mathrm{i}\:\mathrm{dnt}\:\mathrm{knw}\:\mathrm{how}\:\mathrm{it}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{applied}....\:\mathrm{please}\:\mathrm{can}\:\mathrm{you}\: \\ $$$$\mathrm{explain}\:\mathrm{the}\:\mathrm{method}\:\mathrm{and}\:\mathrm{applicatn} \\ $$$$\mathrm{to}\:\mathrm{thiz}\:\mathrm{question}\:\mathrm{if}\:\mathrm{possible}.... \\ $$$$ \\ $$$$ \\ $$$$\mathrm{thanx}\:\mathrm{for}\:\mathrm{always}\:\mathrm{helping}. \\ $$
Commented by chux last updated on 18/Apr/17

$$\mathrm{thanks}\:\mathrm{boss} \\ $$
