
Question and Answers Forum
Question Number 122791 by mohammad17 last updated on 19/Nov/20

Answered by mathmax by abdo last updated on 19/Nov/20

Answered by TANMAY PANACEA last updated on 19/Nov/20
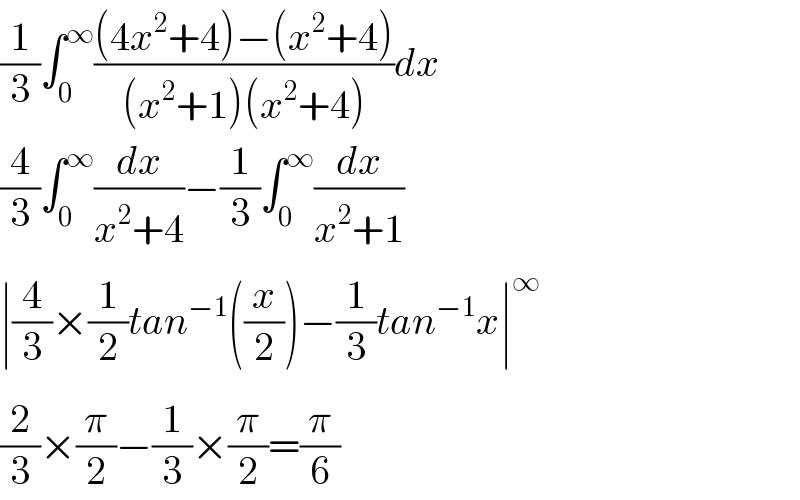
Commented by mohammad17 last updated on 19/Nov/20

Answered by mathmax by abdo last updated on 19/Nov/20
![A =∫_0 ^∞ ((sin^2 x)/x^2 ) dx by parts A =[−((sin^2 x)/x)]_0 ^∞ +∫_0 ^∞ ((2sinx cosx)/x)dx =∫_0 ^∞ ((sin(2x))/x)dx =_(2x=t) ∫_0 ^∞ ((sin(t))/(t/2))×(dt/2) =∫_0 ^∞ ((sint)/t)dt =(π/2)](Q122803.png)
Answered by mathmax by abdo last updated on 19/Nov/20
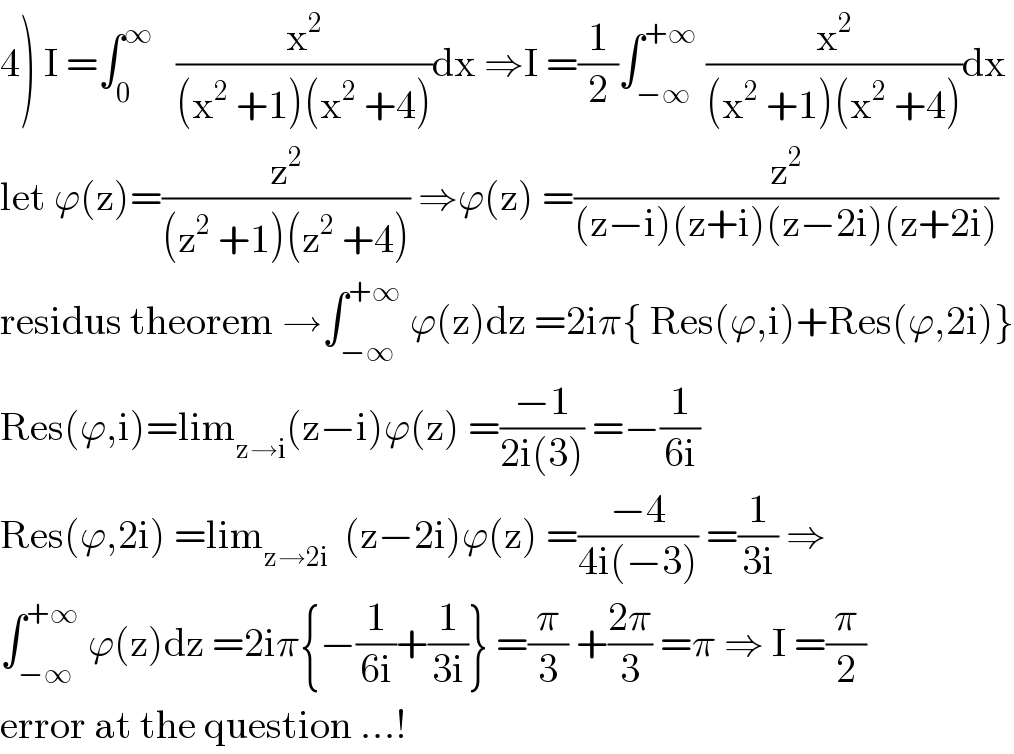
Answered by mathmax by abdo last updated on 19/Nov/20

