
Question and Answers Forum
Question Number 122882 by mnjuly1970 last updated on 20/Nov/20
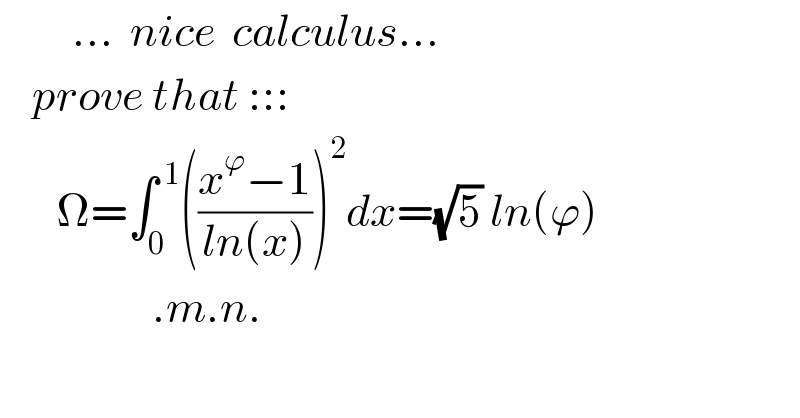
Answered by TANMAY PANACEA last updated on 20/Nov/20
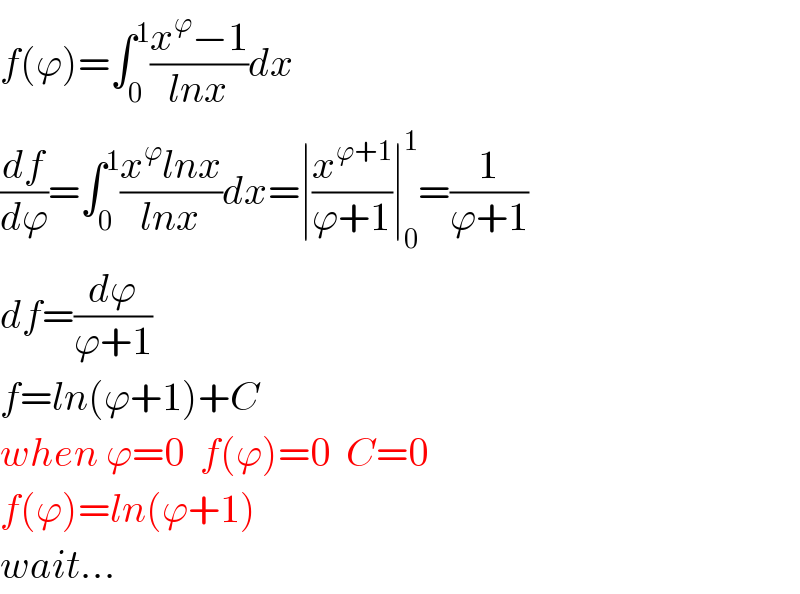
Commented by mnjuly1970 last updated on 21/Nov/20
![thank you mr tanmay for your effort with your permission i present the solution. note :ln(N)=∫_0 ^( 1) ((x^(N−1) −1)/(ln(x)))dx f(a)=∫_0 ^( 1) (((x^a −1)^2 )/(ln^2 (x)))dx f ′(a)=∫_0 ^( 1) (∂/∂a)[(((x^a −1)^2 )/(ln^2 (x)))] =∫_0 ^( 1) ((2(x^a −1)x^a ln(x))/(ln^2 (x)))dx=2∫_0 ^( 1) ((x^(2a) −x^a )/(ln(x)))dx =2∫_0 ^( 1) ((x^(2a) −1)/(ln(x))) +2∫_0 ^( 1) ((1−x^a )/(ln(x)))dx =2ln(2a+1)−2ln(a+1) f(a)=2∫^ ln(2a+1)da−2∫ln(a+1)da+C =(2a+1)ln(2a+1)−(2a+1) −2(a+1)ln(a+1)+2(a+1)+C f(0)=1+C⇒C=−1 f(a)=(2a+1)ln(2a+1)−2(a+1)ln(a+1)+1−1 Ω=f(ϕ)=(2ϕ+1)ln(2ϕ+1)−2(ϕ+1)ln(ϕ+1) ϕ: is golden ratio and we know: ϕ^2 =ϕ+1 =(ϕ^2 +ϕ)ln(ϕ^2 +ϕ)−2ϕ^2 ln(ϕ^2 ) =ϕ^3 ln(ϕ^3 )−4ϕ^2 ln(ϕ) =(3ϕ^3 −4ϕ^2 )ln(ϕ)=(3ϕ^2 +3ϕ−4ϕ^2 )ln(ϕ) =(−ϕ^2 +3ϕ)ln(ϕ)=(−ϕ−1+3ϕ)ln(ϕ) =(2ϕ−1)ln(ϕ)=(2(((1+(√5))/2))−1)ln(ϕ) =(√5) ln(ϕ) ✓ ✓✓](Q122972.png)
| ||
Question and Answers Forum | ||
Question Number 122882 by mnjuly1970 last updated on 20/Nov/20 | ||
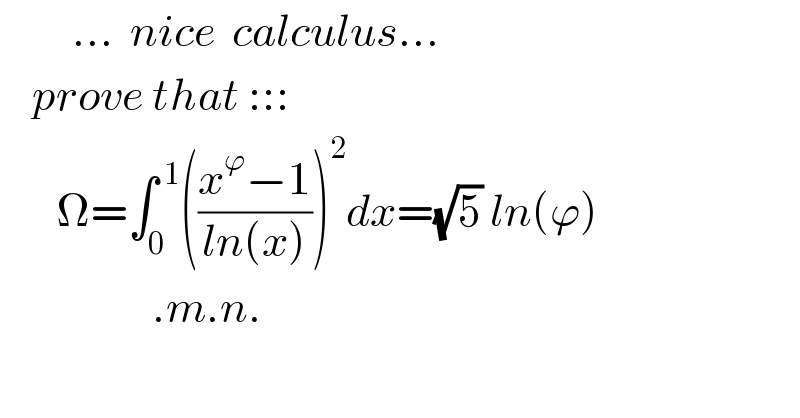 | ||
Answered by TANMAY PANACEA last updated on 20/Nov/20 | ||
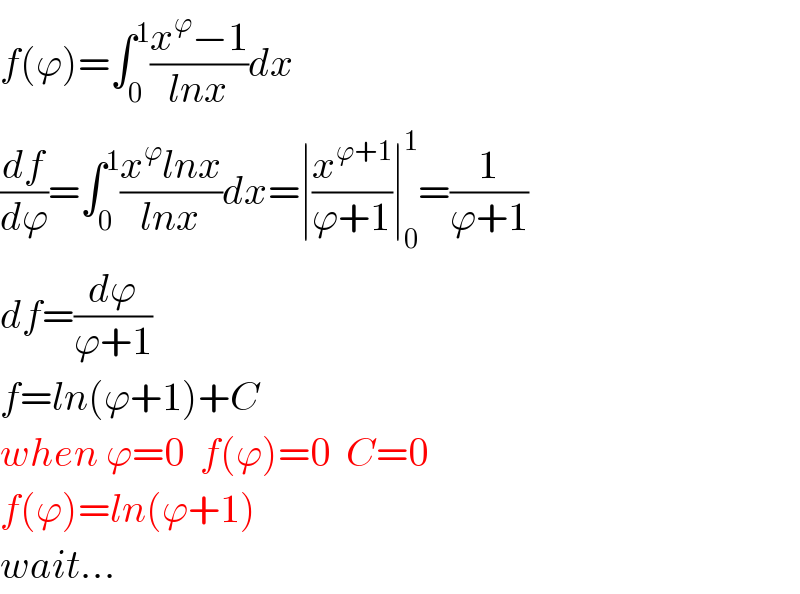 | ||
| ||
Commented by mnjuly1970 last updated on 21/Nov/20 | ||
![thank you mr tanmay for your effort with your permission i present the solution. note :ln(N)=∫_0 ^( 1) ((x^(N−1) −1)/(ln(x)))dx f(a)=∫_0 ^( 1) (((x^a −1)^2 )/(ln^2 (x)))dx f ′(a)=∫_0 ^( 1) (∂/∂a)[(((x^a −1)^2 )/(ln^2 (x)))] =∫_0 ^( 1) ((2(x^a −1)x^a ln(x))/(ln^2 (x)))dx=2∫_0 ^( 1) ((x^(2a) −x^a )/(ln(x)))dx =2∫_0 ^( 1) ((x^(2a) −1)/(ln(x))) +2∫_0 ^( 1) ((1−x^a )/(ln(x)))dx =2ln(2a+1)−2ln(a+1) f(a)=2∫^ ln(2a+1)da−2∫ln(a+1)da+C =(2a+1)ln(2a+1)−(2a+1) −2(a+1)ln(a+1)+2(a+1)+C f(0)=1+C⇒C=−1 f(a)=(2a+1)ln(2a+1)−2(a+1)ln(a+1)+1−1 Ω=f(ϕ)=(2ϕ+1)ln(2ϕ+1)−2(ϕ+1)ln(ϕ+1) ϕ: is golden ratio and we know: ϕ^2 =ϕ+1 =(ϕ^2 +ϕ)ln(ϕ^2 +ϕ)−2ϕ^2 ln(ϕ^2 ) =ϕ^3 ln(ϕ^3 )−4ϕ^2 ln(ϕ) =(3ϕ^3 −4ϕ^2 )ln(ϕ)=(3ϕ^2 +3ϕ−4ϕ^2 )ln(ϕ) =(−ϕ^2 +3ϕ)ln(ϕ)=(−ϕ−1+3ϕ)ln(ϕ) =(2ϕ−1)ln(ϕ)=(2(((1+(√5))/2))−1)ln(ϕ) =(√5) ln(ϕ) ✓ ✓✓](Q122972.png) | ||