Σ_1 ^∞ (((sin (x))/x))=?


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 122883 by kolos last updated on 20/Nov/20

$\sum_{1}^{\infty} (\frac{\sin (x)}{x}) = ?$
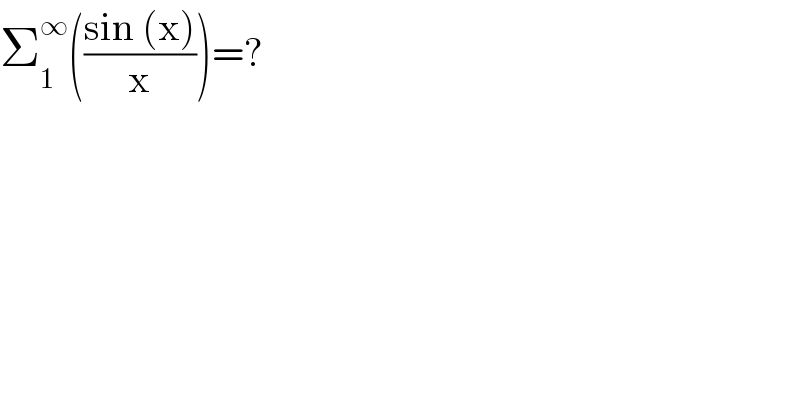
Commented by Dwaipayan Shikari last updated on 20/Nov/20

$\underset{n = 1}{\sum^{\infty}} \frac{s i n x}{x} = \frac{1}{2 i} \underset{n = 1}{\sum^{\infty}} \frac{e^{i x}}{x} - \frac{1}{2 i} \sum^{\infty} \frac{e^{- i x}}{x}$ $= \frac{1}{2 i} (- l o g (1 - e^{i}) + l o g (1 - e^{- i})) = \frac{1}{2 i} l o g (\frac{1 - e^{- i}}{1 - e^{i}})$ $= \frac{1}{2 i} l o g (- e^{- i}) = \frac{1}{2 i} l o g (e^{i π}) + \frac{1}{2 i} ({l o g e}^{- i}) = \frac{π}{2} - \frac{1}{2}$
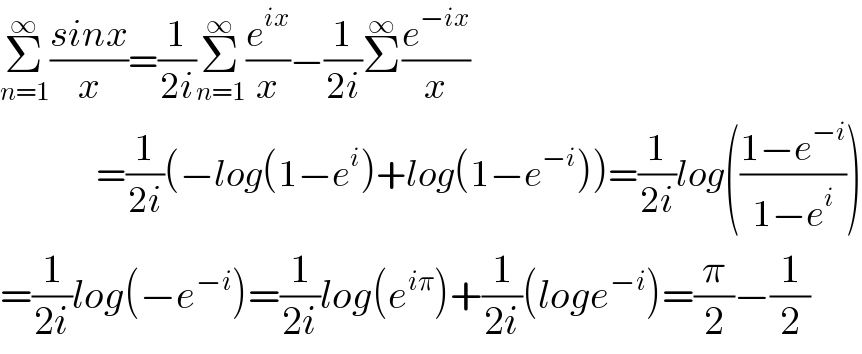
Commented by kolos last updated on 21/Nov/20

$t h a n k s o m u c h, e v e r y s i n g l e o n e$
	Answered by TANMAY PANACEA last updated on 20/Nov/20
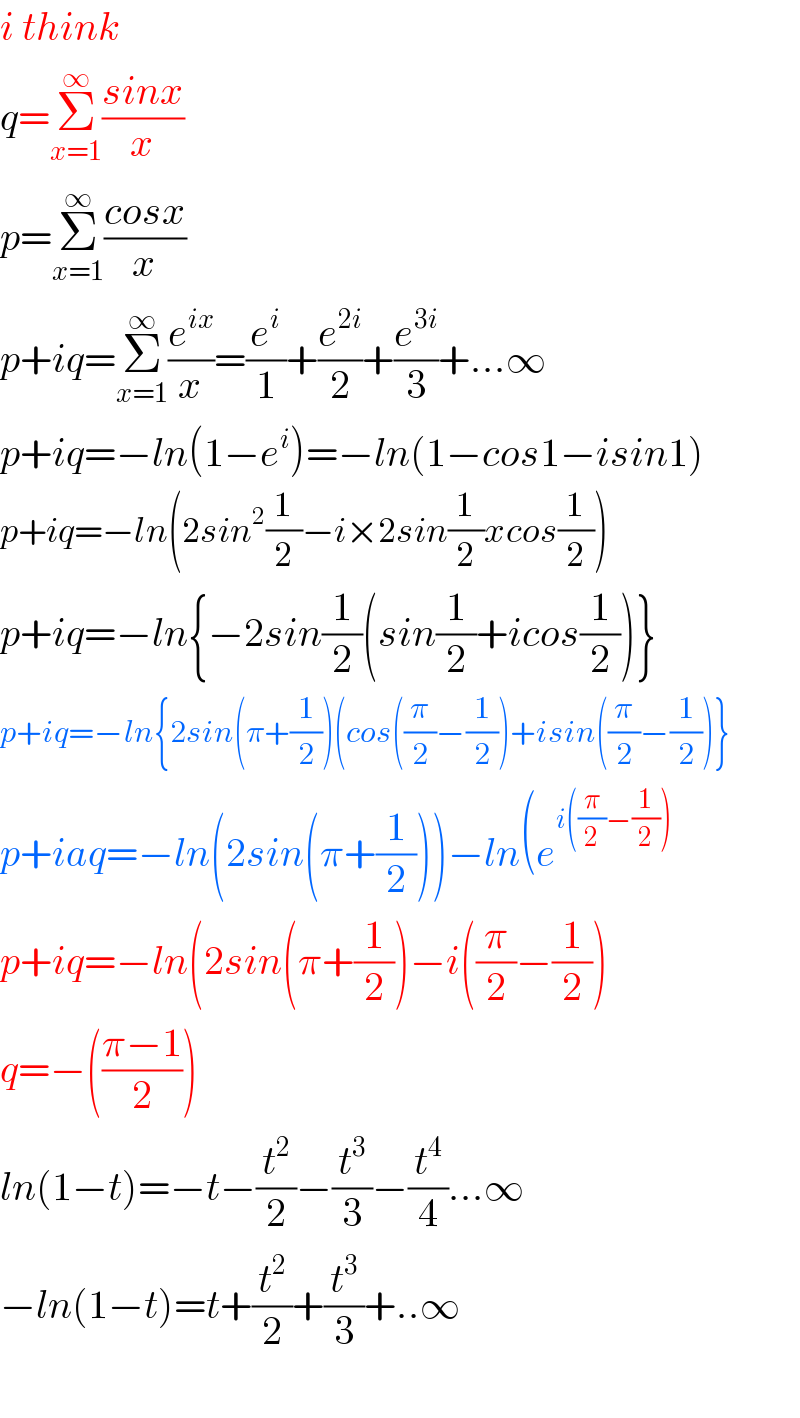
	$i think q=Σ_(x=1) ^∞ ((sinx)/x) p=Σ_(x=1) ^∞ ((cosx)/x) p+iq=Σ_(x=1) ^∞ (e^(ix) /x)=(e^i /1)+(e^(2i) /2)+(e^(3i) /3)+...∞ p+iq=−ln(1−e^i )=−ln(1−cos1−isin1) p+iq=−ln(2sin^2 (1/2)−i×2sin(1/2)xcos(1/2)) p+iq=−ln{−2sin(1/2)(sin(1/2)+icos(1/2))} p+iq=−ln{2sin(π+(1/2))(cos((π/2)−(1/2))+isin((π/2)−(1/2))} p+iaq=−ln(2sin(π+(1/2)))−ln(e^(i((π/2)−(1/2))) p+iq=−ln(2sin(π+(1/2))−i((π/2)−(1/2)) q=−(((π−1)/2)) ln(1−t)=−t−(t^2 /2)−(t^3 /3)−(t^4 /4)...∞ −ln(1−t)=t+(t^2 /2)+(t^3 /3)+..∞$
	$i t h i n k$ $q = \underset{x = 1}{\sum^{\infty}} \frac{s i n x}{x}$ $p = \underset{x = 1}{\sum^{\infty}} \frac{c o s x}{x}$ $p + i q = \underset{x = 1}{\sum^{\infty}} \frac{e^{i x}}{x} = \frac{e^{i}}{1} + \frac{e^{2 i}}{2} + \frac{e^{3 i}}{3} + . . . \infty$ $p + i q = - l n (1 - e^{i}) = - l n (1 - c o s 1 - i s i n 1)$ $p + i q = - l n (2 {s i n}^{2} \frac{1}{2} - i \times 2 s i n \frac{1}{2} x c o s \frac{1}{2})$ $p + i q = - l n {- 2 s i n \frac{1}{2} (s i n \frac{1}{2} + i c o s \frac{1}{2})}$ $p + i q = - l n {2 s i n (π + \frac{1}{2}) (c o s (\frac{π}{2} - \frac{1}{2}) + i s i n (\frac{π}{2} - \frac{1}{2})}$ $p + i a q = - l n (2 s i n (π + \frac{1}{2})) - l n (e^{i (\frac{π}{2} - \frac{1}{2})}$ $p + i q = - l n (2 s i n (π + \frac{1}{2}) - i (\frac{π}{2} - \frac{1}{2})$ $q = - (\frac{π - 1}{2})$ $l n (1 - t) = - t - \frac{t^{2}}{2} - \frac{t^{3}}{3} - \frac{t^{4}}{4} . . . \infty$ $- l n (1 - t) = t + \frac{t^{2}}{2} + \frac{t^{3}}{3} + . . \infty$
	Answered by Dwaipayan Shikari last updated on 20/Nov/20

	$I n t h e s a m e w a y$ $\underset{n = 1}{\sum^{\infty}} \frac{c o s x}{x} = \frac{1}{2} \underset{n = 1}{\sum^{\infty}} \frac{e^{i x}}{x} + \frac{e^{- i x}}{x} = \frac{1}{2} (l o g (\frac{1}{(1 - e^{i}) (1 - e^{- i})})$ $= \frac{1}{2} l o g (\frac{1}{1 - (e^{i} + e^{- i}) + 1}) = \frac{1}{2} l o g (\frac{1}{2 - 2 c o s (1)})$
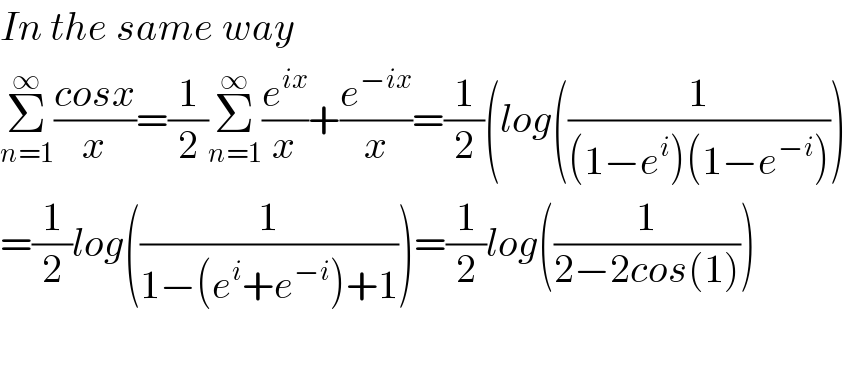
	Answered by mathmax by abdo last updated on 21/Nov/20

	$i think the Q is \sum_{n = 1}^{\infty} \frac{\sin (n)}{n}$ $let S (x) = \sum_{n = 1}^{\infty} \frac{\sin (nx)}{n} \Rightarrow S (x) = Im (\sum_{n = 1}^{\infty} \frac{e^{inx}}{n})$ $w (x) = \sum_{n = 1}^{\infty} \frac{e^{inx}}{n} \Rightarrow w^{^{'}} (x) = \sum_{n = 1}^{\infty} \frac{in e^{inx}}{n} = i \sum_{n = 1}^{\infty} {(e^{ix})}^{n}$ $= i \times \frac{1}{1 - e^{ix}} \Rightarrow w (x) = - \ln (1 - e^{ix}) + c with w) 0) = 0 = c \Rightarrow$ $w (x) = - \ln (1 - e^{ix}) \Rightarrow S (x) = Im (- \ln (1 - e^{ix})) we have$ $\ln (1 - e^{ix}) = \ln (1 - cosx - isinx) = \ln ({2 \sin}^{2} (\frac{x}{2}) - 2 isin (\frac{x}{2}) \cos (\frac{x}{2}))$ $= \ln (2) + \ln (- isin (\frac{x}{2}) (\cos (\frac{x}{2}) + isin (\frac{x}{2})) = \ln (2) + \ln (- i) + \ln (\sin (\frac{x}{2})) + \ln (e^{\frac{ix}{2}})$ $= \ln (2) - \frac{i π}{2} + \ln (\sin (\frac{x}{2})) + \frac{ix}{2} = \ln (2 \sin (\frac{x}{2})) + \frac{x - π}{2} i \Rightarrow$ $S (x) = \frac{π - x}{2} \Rightarrow \sum_{n = 1}^{\infty} \frac{\sin (n)}{n} = S (1) = \frac{π - 1}{2}$
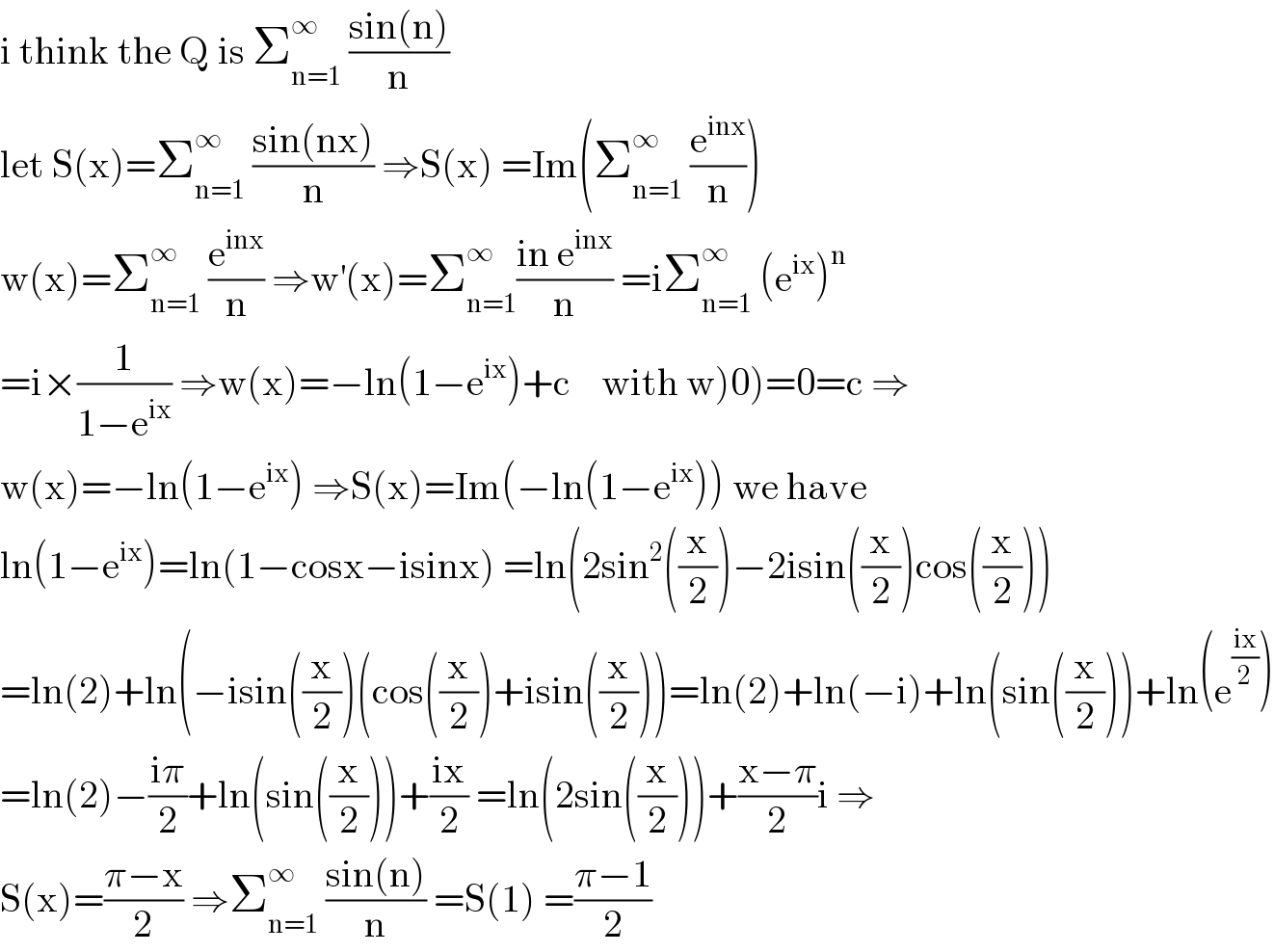
	Answered by mnjuly1970 last updated on 21/Nov/20

	$Φ = \underset{n = 1}{\sum^{\infty}} (\frac{s i n (n)}{n}) = \frac{1}{2 i} \underset{n = 1}{\sum^{\infty}} (\frac{e^{i n} - e^{- i n}}{n})$ $= \frac{1}{2 i} [- l n (1 - e^{i}) + l n (1 - e^{- i})]$ $= \frac{1}{2 i} l n (\frac{1 - e^{- i}}{1 - e^{i}}) = \frac{1}{2 i} l n (- e^{- i})$ $= \frac{1}{2 i} [i π - i] = \frac{π - 1}{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum