Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 122885 by CanovasCamiseros last updated on 20/Nov/20

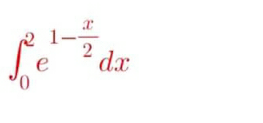
Commented by CanovasCamiseros last updated on 20/Nov/20

Please help

Pleasehelp

Answered by ebi last updated on 20/Nov/20

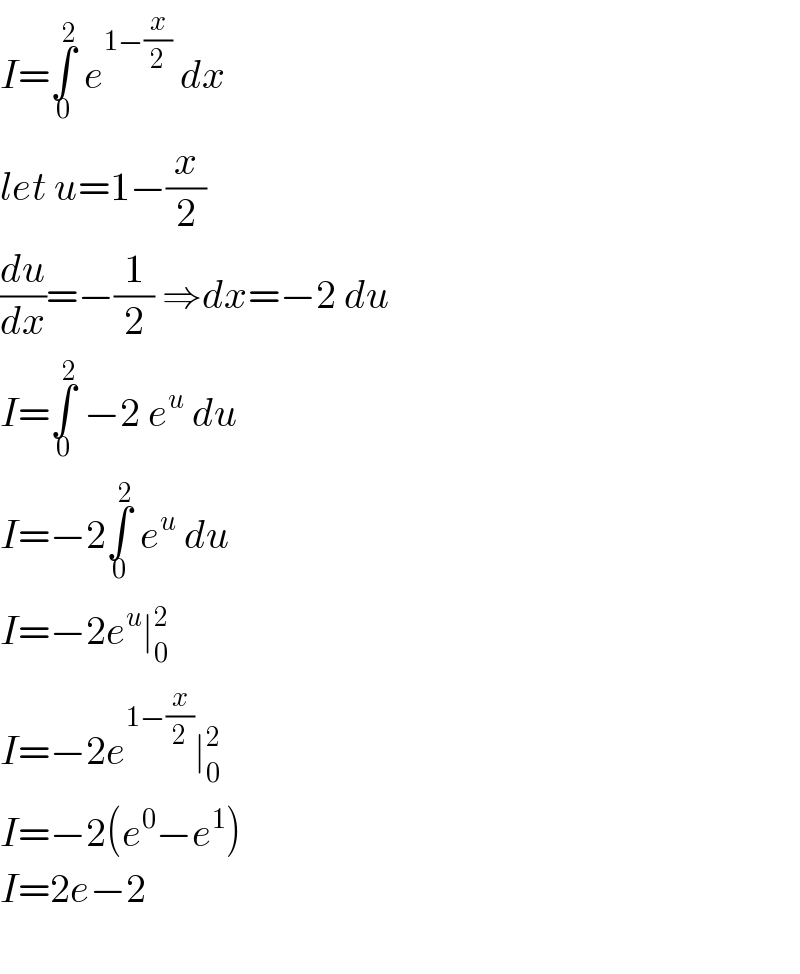
I=∫_0 ^2 e^(1−(x/2)) dx let u=1−(x/2) (du/dx)=−(1/2) ⇒dx=−2 du I=∫_0 ^2 −2 e^u du I=−2∫_0 ^2 e^u du I=−2e^u ∣_0 ^2 I=−2e^(1−(x/2)) ∣_0 ^2 I=−2(e^0 −e^1 ) I=2e−2

I=∫20e1−x2dxletu=1−x2dudx=−12⇒dx=−2duI=∫20−2euduI=−2∫20euduI=−2eu∣02I=−2e1−x2∣02I=−2(e0−e1)I=2e−2

Answered by MJS_new last updated on 20/Nov/20

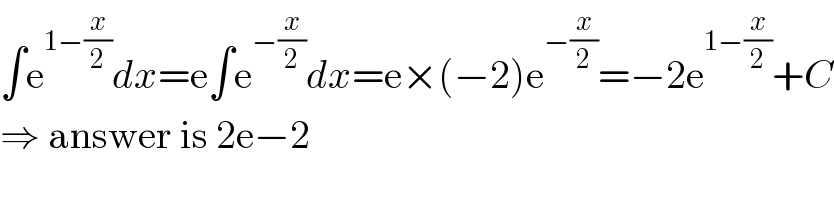
∫e^(1−(x/2)) dx=e∫e^(−(x/2)) dx=e×(−2)e^(−(x/2)) =−2e^(1−(x/2)) +C ⇒ answer is 2e−2

∫e1−x2dx=e∫e−x2dx=e×(−2)e−x2=−2e1−x2+C⇒answeris2e−2

Answered by Bird last updated on 20/Nov/20

I=∫_0 ^2 e^(1−(x/2)) dx ⇒I=_((x/2)=t) ∫_0 ^1 e^(1−t) 2dt =2e ∫_0 ^(1 ) e^(−t) dt =2e[−e^(−t) ]_0 ^1 =2e{1−e^(−1) } =2e−2

I=∫02e1−x2dx⇒I=x2=t∫01e1−t2dt=2e∫01e−tdt=2e[−e−t]01=2e{1−e−1}=2e−2

Terms of Service

Privacy Policy

Contact: info@tinkutara.com