Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 1229 by Rasheed Soomro last updated on 16/Jul/15

f( f(x) )=x^2 −x+1 f(x)=? (Modification of Q 1147)

$${f}\left(\:{f}\left({x}\right)\:\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({x}\right)=? \\ $$$$\left({Modification}\:{of}\:{Q}\:\mathrm{1147}\right) \\ $$

Commented by 123456 last updated on 17/Jul/15

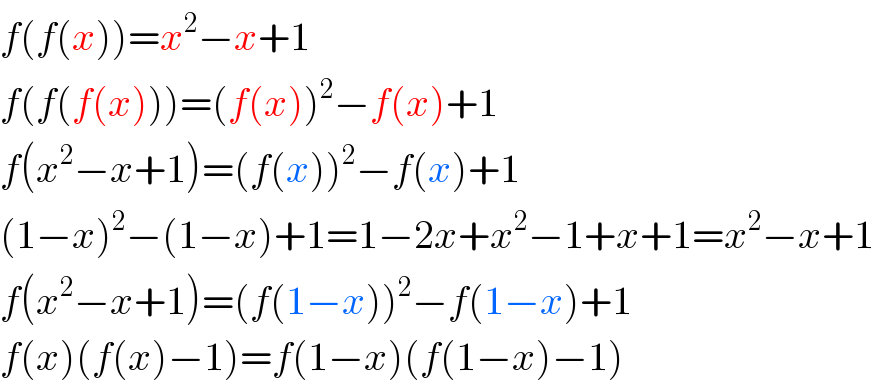
f(f(x))=x^2 −x+1 f(f(f(x)))=(f(x))^2 −f(x)+1 f(x^2 −x+1)=(f(x))^2 −f(x)+1 (1−x)^2 −(1−x)+1=1−2x+x^2 −1+x+1=x^2 −x+1 f(x^2 −x+1)=(f(1−x))^2 −f(1−x)+1 f(x)(f(x)−1)=f(1−x)(f(1−x)−1)

$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({f}\left({f}\left({x}\right)\right)\right)=\left({f}\left({x}\right)\right)^{\mathrm{2}} −{f}\left({x}\right)+\mathrm{1} \\ $$$${f}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\left({f}\left({x}\right)\right)^{\mathrm{2}} −{f}\left({x}\right)+\mathrm{1} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{2}} −\left(\mathrm{1}−{x}\right)+\mathrm{1}=\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} −\mathrm{1}+{x}+\mathrm{1}={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\left({f}\left(\mathrm{1}−{x}\right)\right)^{\mathrm{2}} −{f}\left(\mathrm{1}−{x}\right)+\mathrm{1} \\ $$$${f}\left({x}\right)\left({f}\left({x}\right)−\mathrm{1}\right)={f}\left(\mathrm{1}−{x}\right)\left({f}\left(\mathrm{1}−{x}\right)−\mathrm{1}\right) \\ $$

Commented by Rasheed Ahmad last updated on 18/Jul/15

Dear 123456 I understood your logic with some difficulty.Actually your explanation lacks in−between instructions badly.Pl put some instructions for clarification and also insert some more steps in order to to be understood easily. Anyway now after understanding I appreciate your logic.

$${Dear}\:\mathrm{123456} \\ $$$${I}\:{understood}\:{your}\:{logic}\:{with}\: \\ $$$${some}\:{difficulty}.{Actually}\:{your}\: \\ $$$${explanation}\:{lacks}\:{in}−{between}\:{instructions} \\ $$$${badly}.{Pl}\:{put}\:{some}\:{instructions}\: \\ $$$${for}\:{clarification}\:{and}\:{also}\:{insert}\: \\ $$$${some}\:{more}\:{steps}\:{in}\:{order}\:{to}\: \\ $$$${to}\:{be}\:{understood}\:{easily}. \\ $$$${Anyway}\:{now}\:{after}\:{understanding} \\ $$$${I}\:{appreciate}\:{your}\:{logic}. \\ $$

Commented by Rasheed Ahmad last updated on 17/Jul/15

Very good rule and very nice feature you have discovered: Rule: d(f•f)= [d(f)]^2 feature: f( f(x) )=f( f(1−x) ) Appreciation for you!

$${Very}\:{good}\:{rule}\:{and}\:{very}\:{nice}\: \\ $$$${feature}\:{you}\:{have}\:{discovered}: \\ $$$${Rule}:\:{d}\left({f}\bullet{f}\right)=\:\left[{d}\left({f}\right)\right]^{\mathrm{2}} \\ $$$${feature}:\:\:{f}\left(\:{f}\left({x}\right)\:\right)={f}\left(\:{f}\left(\mathrm{1}−{x}\right)\:\right) \\ $$$${Appreciation}\:{for}\:{you}! \\ $$

Commented by Rasheed Ahmad last updated on 17/Jul/15

It can be proved that f(x) is not a polynomial.

$${It}\:{can}\:{be}\:{proved}\:{that}\:{f}\left({x}\right)\:{is}\:{not}\:{a} \\ $$$${polynomial}. \\ $$

Commented by 123456 last updated on 17/Jul/15

yes, because if d(f) is the degree of f then the degree of f•f is d(f•f)=[d(f)]^2 then [d(f)]^2 =2⇒d(f)=(√2) wich is impossible however its have some symetry, you easy can see that f(f(x))=f(f(1−x))

$$\mathrm{yes},\:\mathrm{because}\:\mathrm{if}\:\mathrm{d}\left({f}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{degree}\:\mathrm{of}\:{f} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{degree}\:\mathrm{of}\:{f}\bullet{f}\:\mathrm{is}\:\mathrm{d}\left({f}\bullet{f}\right)=\left[\mathrm{d}\left({f}\right)\right]^{\mathrm{2}} \\ $$$$\mathrm{then} \\ $$$$\left[\mathrm{d}\left({f}\right)\right]^{\mathrm{2}} =\mathrm{2}\Rightarrow\mathrm{d}\left({f}\right)=\sqrt{\mathrm{2}} \\ $$$$\mathrm{wich}\:\mathrm{is}\:\mathrm{impossible} \\ $$$$\mathrm{however}\:\mathrm{its}\:\mathrm{have}\:\mathrm{some}\:\mathrm{symetry},\:\mathrm{you}\:\mathrm{easy} \\ $$$$\mathrm{can}\:\mathrm{see}\:\mathrm{that} \\ $$$${f}\left({f}\left({x}\right)\right)={f}\left({f}\left(\mathrm{1}−{x}\right)\right) \\ $$

Commented by 123456 last updated on 19/Jul/15

f(0)=1(from Q1147) f(1)=1(from Q1147) claim 1:f(x)=1 only if x=0 or x=1 proof: suppose there are some x∉{0,1} such that f(x)=1, then f(f(x))=x^2 −x+1 f(1)=x^2 −x+1 1=x^2 −x+1 x^2 −x=0 x(x−1)=0 x=0∨x=1 contradiction with the fact that x∉{0,1} claim 2:f(0)=1 suppose that f(0)=a with a∉{0,1} f(f(x))=x^2 −x+1 f(f(0))=1 (x=0) f(a)=1 contradction with claim 1. but a≠0, because if a=0, then f(f(0))=1 f(0)=1 contradiction with f(0)=a=0 claim 3:∄x,f(x)=0 suppose that there is some x that f(x)=0, then f(f(x))=x^2 −x+1 f(0)=x^2 −x+1 by claim 2 1=x^2 −x+1 x=0∨x=1 contradction with f(0)=f(1)=1 claim 4:f(x)=x only for x=1 suppose that f(x)=x for some x≠1, then f(f(x))=x^2 −x+1 f(x)=x^2 −x+1 x=x^2 −x+1 x^2 −2x+1=0 (x−1)^2 =0 x=1 wich contradict the fact that x≠1 −−−−−−−−−−−−− x^2 −x+1=0 Δ=(−1)^2 −4(1)(1)=1−4=−3 x=((−(−1)±(√(−3)))/(2(1)))=((1±i(√3))/2)=e^(±iπ/3) −−−−−−−−−−−−−−−− f(f(x))=x^2 −x+1 f(x)=y f(y)=x^2 −x+1 f(f(f(x)))=(f(x))^2 −f(x)+1 f(f(y))=y^2 −y+1 f(y)=z f(z)=y^2 −y+1 −−−−−−−−−−−−−−−− f(f(1/2))=3/4 f(3/4)=(f(1/2))^2 −f(1/2)+1

$${f}\left(\mathrm{0}\right)=\mathrm{1}\left(\mathrm{from}\:\mathrm{Q1147}\right) \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}\left(\mathrm{from}\:\mathrm{Q1147}\right) \\ $$$$\mathrm{claim}\:\mathrm{1}:{f}\left({x}\right)=\mathrm{1}\:\mathrm{only}\:\mathrm{if}\:{x}=\mathrm{0}\:\mathrm{or}\:{x}=\mathrm{1} \\ $$$$\mathrm{proof}: \\ $$$$\mathrm{suppose}\:\mathrm{there}\:\mathrm{are}\:\mathrm{some}\:{x}\notin\left\{\mathrm{0},\mathrm{1}\right\}\:\mathrm{such}\:\mathrm{that}\:{f}\left({x}\right)=\mathrm{1},\:\mathrm{then} \\ $$$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$$\mathrm{1}={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${x}^{\mathrm{2}} −{x}=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\vee{x}=\mathrm{1} \\ $$$$\mathrm{contradiction}\:\mathrm{with}\:\mathrm{the}\:\mathrm{fact}\:\mathrm{that}\:{x}\notin\left\{\mathrm{0},\mathrm{1}\right\} \\ $$$$\mathrm{claim}\:\mathrm{2}:{f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{suppose}\:\mathrm{that}\:{f}\left(\mathrm{0}\right)={a}\:\mathrm{with}\:{a}\notin\left\{\mathrm{0},\mathrm{1}\right\} \\ $$$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({f}\left(\mathrm{0}\right)\right)=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({x}=\mathrm{0}\right) \\ $$$${f}\left({a}\right)=\mathrm{1} \\ $$$$\mathrm{contradction}\:\mathrm{with}\:\mathrm{claim}\:\mathrm{1}. \\ $$$$\mathrm{but}\:{a}\neq\mathrm{0},\:\mathrm{because}\:\mathrm{if}\:{a}=\mathrm{0},\:\mathrm{then} \\ $$$${f}\left({f}\left(\mathrm{0}\right)\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{contradiction}\:\mathrm{with}\:{f}\left(\mathrm{0}\right)={a}=\mathrm{0} \\ $$$$\mathrm{claim}\:\mathrm{3}:\nexists{x},{f}\left({x}\right)=\mathrm{0} \\ $$$$\mathrm{suppose}\:\mathrm{that}\:\mathrm{there}\:\mathrm{is}\:\mathrm{some}\:{x}\:\mathrm{that}\:{f}\left({x}\right)=\mathrm{0},\:\mathrm{then} \\ $$$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$$\mathrm{by}\:\mathrm{claim}\:\mathrm{2} \\ $$$$\mathrm{1}={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${x}=\mathrm{0}\vee{x}=\mathrm{1} \\ $$$$\mathrm{contradction}\:\mathrm{with}\:{f}\left(\mathrm{0}\right)={f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{claim}\:\mathrm{4}:{f}\left({x}\right)={x}\:\mathrm{only}\:\mathrm{for}\:{x}=\mathrm{1} \\ $$$$\mathrm{suppose}\:\mathrm{that}\:\mathrm{f}\left({x}\right)={x}\:\mathrm{for}\:\mathrm{some}\:{x}\neq\mathrm{1},\:\mathrm{then} \\ $$$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${x}={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\mathrm{1} \\ $$$$\mathrm{wich}\:\mathrm{contradict}\:\mathrm{the}\:\mathrm{fact}\:\mathrm{that}\:{x}\neq\mathrm{1} \\ $$$$−−−−−−−−−−−−− \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{1}\right)=\mathrm{1}−\mathrm{4}=−\mathrm{3} \\ $$$${x}=\frac{−\left(−\mathrm{1}\right)\pm\sqrt{−\mathrm{3}}}{\mathrm{2}\left(\mathrm{1}\right)}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\pm{i}\pi/\mathrm{3}} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${f}\left({f}\left({x}\right)\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({x}\right)={y} \\ $$$${f}\left({y}\right)={x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$${f}\left({f}\left({f}\left({x}\right)\right)\right)=\left({f}\left({x}\right)\right)^{\mathrm{2}} −{f}\left({x}\right)+\mathrm{1} \\ $$$${f}\left({f}\left({y}\right)\right)={y}^{\mathrm{2}} −{y}+\mathrm{1} \\ $$$${f}\left({y}\right)={z} \\ $$$${f}\left({z}\right)={y}^{\mathrm{2}} −{y}+\mathrm{1} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${f}\left({f}\left(\mathrm{1}/\mathrm{2}\right)\right)=\mathrm{3}/\mathrm{4} \\ $$$${f}\left(\mathrm{3}/\mathrm{4}\right)=\left({f}\left(\mathrm{1}/\mathrm{2}\right)\right)^{\mathrm{2}} −{f}\left(\mathrm{1}/\mathrm{2}\right)+\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com