
Question and Answers Forum
Question Number 122927 by bemath last updated on 21/Nov/20

Commented by liberty last updated on 21/Nov/20
![μ(x)=∫ (√((1−(√x))/(1+(√x)))) dx [ let (√x) = sin z ⇒ dx = sin 2z dz ] μ(x)=∫ (√((1−sin z)/(1+sin z))) (sin 2z dz ) μ(x)=∫ ((√((1−sin z)^2 ))/(cos z)) (2sin z cos z ) dz μ(x)= ∫ 2sin z(1−sin z) dz μ(x)=∫(2sin z−2((1/2)−cos 2z))dz μ(x)=−2cos z−z+sin 2z + c μ(x)=2cos z(sin z−1)−z + c μ(x)=2(√(1−x)) ((√x) −1)−sin^(−1) (√x) + c](Q122929.png)
Answered by MJS_new last updated on 21/Nov/20
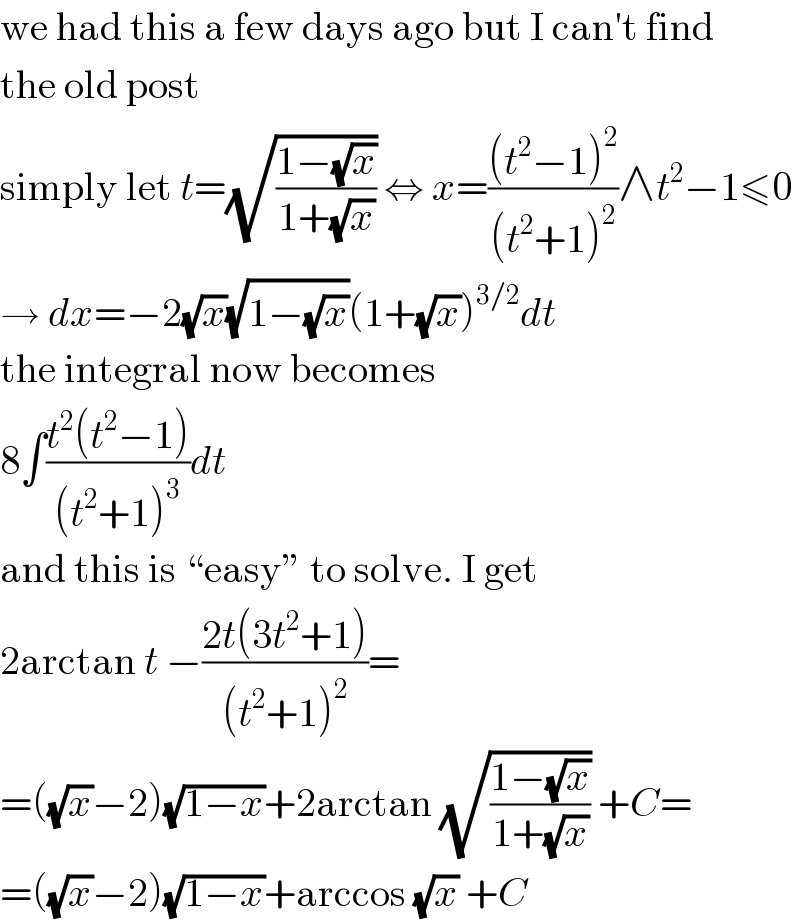
| ||
Question and Answers Forum | ||
Question Number 122927 by bemath last updated on 21/Nov/20 | ||
 | ||
Commented by liberty last updated on 21/Nov/20 | ||
![μ(x)=∫ (√((1−(√x))/(1+(√x)))) dx [ let (√x) = sin z ⇒ dx = sin 2z dz ] μ(x)=∫ (√((1−sin z)/(1+sin z))) (sin 2z dz ) μ(x)=∫ ((√((1−sin z)^2 ))/(cos z)) (2sin z cos z ) dz μ(x)= ∫ 2sin z(1−sin z) dz μ(x)=∫(2sin z−2((1/2)−cos 2z))dz μ(x)=−2cos z−z+sin 2z + c μ(x)=2cos z(sin z−1)−z + c μ(x)=2(√(1−x)) ((√x) −1)−sin^(−1) (√x) + c](Q122929.png) | ||
Answered by MJS_new last updated on 21/Nov/20 | ||
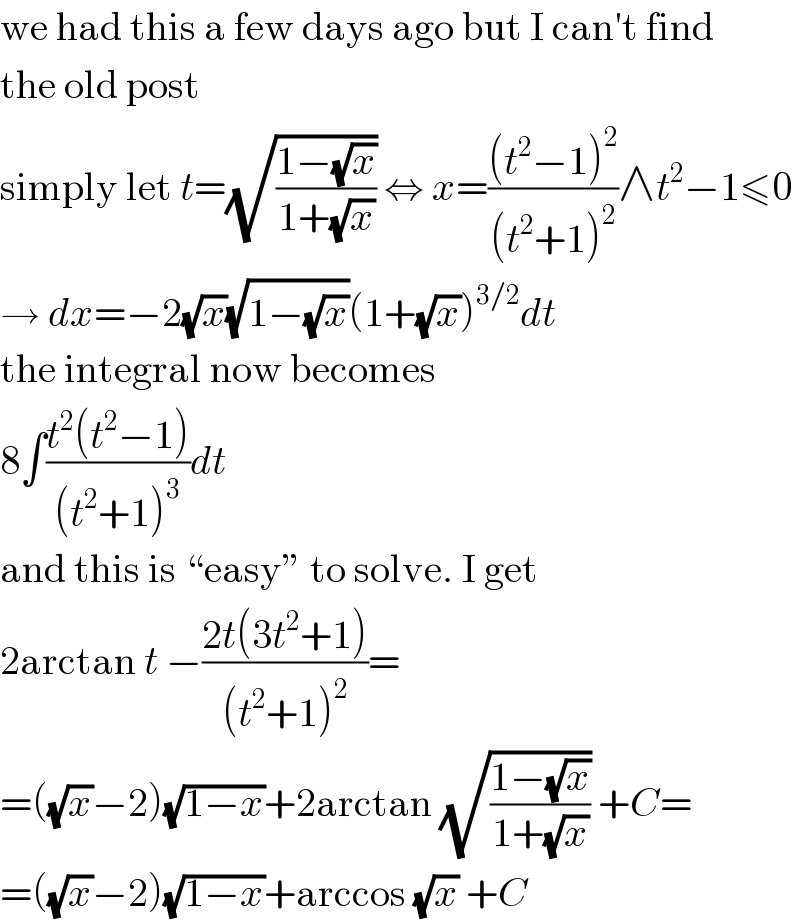 | ||
| ||