
Question and Answers Forum
Question Number 122963 by Lordose last updated on 21/Nov/20
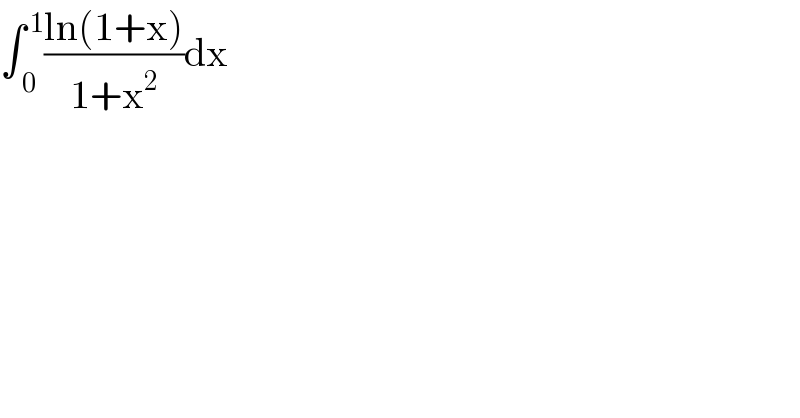
Answered by Dwaipayan Shikari last updated on 21/Nov/20
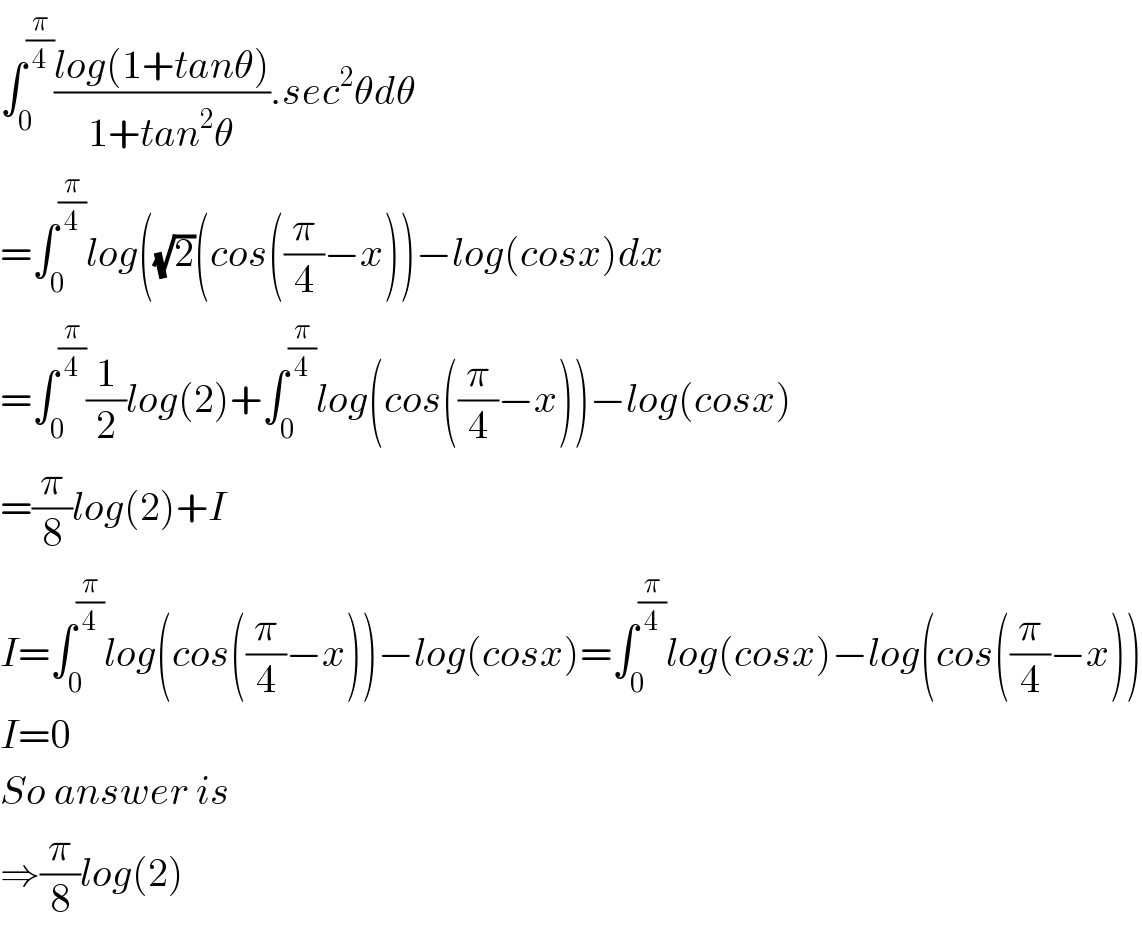
Answered by mnjuly1970 last updated on 21/Nov/20
![solution: x=tan(y)⇒ dx= (1+tan^2 (y))dy I =∫_0 ^( 1) ((ln(1+x))/(1+x^2 ))dx=∫_0 ^( (π/4)) ln(1+tan(y))dy =∫_0 ^( (π/4)) ln[1+tan((π/4)−y)]dy =∫_0 ^( (π/4)) ln(1+((1−tan(y))/(1+tan(y))))dy =∫_0 ^( (π/4)) {ln(2)−ln(1+tan(y))}dy =(π/4)ln(2)−I 2I=(π/4)ln(2) ⇒I=(π/8)ln(2) ✓](Q122966.png)
| ||
Question and Answers Forum | ||
Question Number 122963 by Lordose last updated on 21/Nov/20 | ||
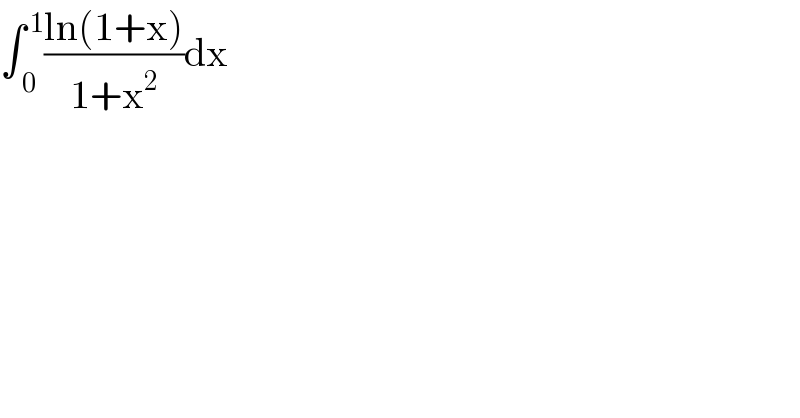 | ||
Answered by Dwaipayan Shikari last updated on 21/Nov/20 | ||
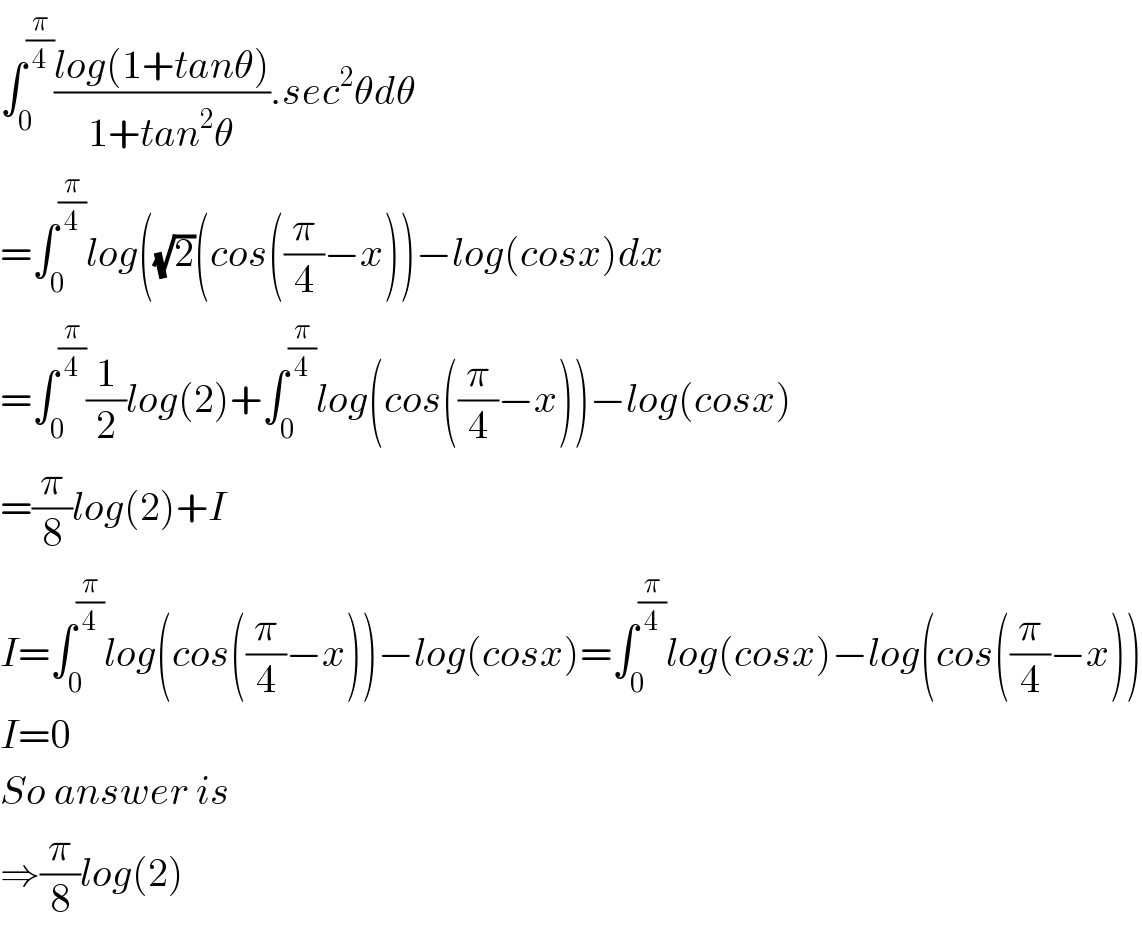 | ||
| ||
Answered by mnjuly1970 last updated on 21/Nov/20 | ||
![solution: x=tan(y)⇒ dx= (1+tan^2 (y))dy I =∫_0 ^( 1) ((ln(1+x))/(1+x^2 ))dx=∫_0 ^( (π/4)) ln(1+tan(y))dy =∫_0 ^( (π/4)) ln[1+tan((π/4)−y)]dy =∫_0 ^( (π/4)) ln(1+((1−tan(y))/(1+tan(y))))dy =∫_0 ^( (π/4)) {ln(2)−ln(1+tan(y))}dy =(π/4)ln(2)−I 2I=(π/4)ln(2) ⇒I=(π/8)ln(2) ✓](Q122966.png) | ||
| ||