
Question Number 12304 by Gaurav3651 last updated on 18/Apr/17
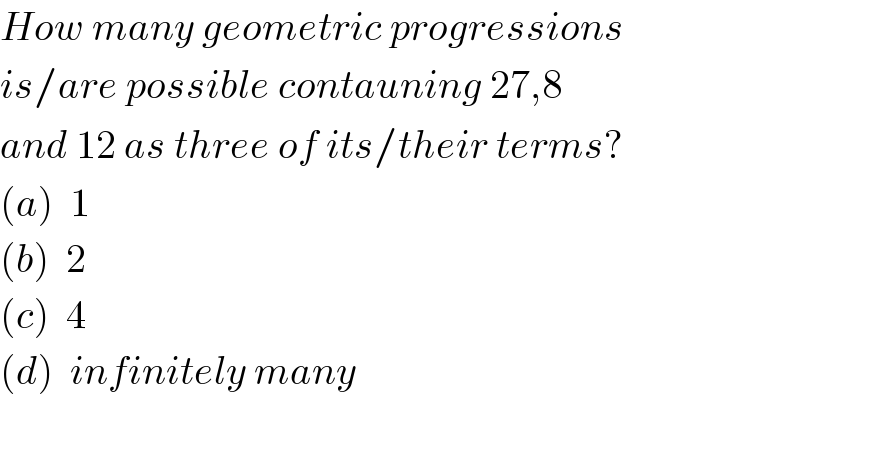
$${How}\:{many}\:{geometric}\:{progressions} \\ $$$${is}/{are}\:{possible}\:{contauning}\:\mathrm{27},\mathrm{8} \\ $$$${and}\:\mathrm{12}\:{as}\:{three}\:{of}\:{its}/{their}\:{terms}? \\ $$$$\left({a}\right)\:\:\mathrm{1} \\ $$$$\left({b}\right)\:\:\mathrm{2} \\ $$$$\left({c}\right)\:\:\mathrm{4} \\ $$$$\left({d}\right)\:\:{infinitely}\:{many} \\ $$$$ \\ $$
Answered by mrW1 last updated on 18/Apr/17

$${let}'{s}\:{assume}\:\mathrm{8},\:\mathrm{12}\:{and}\:\mathrm{27}\:{are}\:\mathrm{3}\:{terms}\:{of} \\ $$$${a}\:{GP}\:{with}\:{the}\:{common}\:{ratio}\:{q}: \\ $$$$\mathrm{8}...\left({n}−\mathrm{1}\:{terms}\right)...\mathrm{12}....\left({m}−\mathrm{1}\:{terms}\right)...\mathrm{27} \\ $$$$ \\ $$$$\frac{\mathrm{27}}{\mathrm{12}}=\frac{\mathrm{3}×\mathrm{3}×\mathrm{3}}{\mathrm{3}×\mathrm{2}×\mathrm{2}}=\frac{\mathrm{3}×\mathrm{3}}{\mathrm{2}×\mathrm{2}}={q}^{{m}} \:\:\:\:\:\:\:\:\left({i}\right) \\ $$$$\frac{\mathrm{12}}{\mathrm{8}}=\frac{\mathrm{2}×\mathrm{2}×\mathrm{3}}{\mathrm{2}×\mathrm{2}×\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}={q}^{{n}} \:\:\:\:\:\:\:\:\:\:\:\:\:\left({ii}\right) \\ $$$${q}^{{m}−{n}} =\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\left({i}\right)/\left({ii}\right) \\ $$$$\Rightarrow\:{q}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{m}−{n}}} \\ $$$${q}^{{n}} =\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{{n}}{{m}−{n}}} =\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:{from}\:\left({ii}\right) \\ $$$$\Rightarrow\:\frac{{n}}{{m}−{n}}=\mathrm{1} \\ $$$${n}={m}−{n} \\ $$$$\Rightarrow\:{m}=\mathrm{2}{n} \\ $$$$\Rightarrow\:{q}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{n}}} \:\:\:\:\:\:{from}\:\left({ii}\right) \\ $$$${i}.{e}.\:\:{for}\:{any}\:{n}\geqslant\mathrm{1}\:{we}\:{can}\:{always}\:{find} \\ $$$${a}\:{GP}\:\:{whose}\:\mathrm{1}{st}\:{term}\:{is}\:\mathrm{8},\:\left(\mathrm{1}+{n}\right)−{th}\: \\ $$$${term}\:{is}\:\mathrm{12}\:{and}\:\left(\mathrm{1}+\mathrm{3}{n}\right)−{th}\:{term}\:{is}\:\mathrm{27}, \\ $$$${and}\:{their}\:{common}\:{ratio}\:{is}\:{q}=\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{n}}} : \\ $$$${T}_{\mathrm{1}} =\mathrm{8} \\ $$$$.....\:\left({n}−\mathrm{1}\:{terms}\:{between}\right) \\ $$$${T}_{\mathrm{1}+{n}} =\mathrm{8}×{q}^{{n}} =\mathrm{8}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{{n}}{{n}}} =\mathrm{12} \\ $$$$.....\:\left(\mathrm{2}{n}−\mathrm{1}\:{terms}\:{between}\right) \\ $$$${T}_{\mathrm{1}+\mathrm{3}{n}} =\mathrm{8}×{q}^{\mathrm{3}{n}} =\mathrm{8}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{3}{n}}{{n}}} =\mathrm{8}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{27}\: \\ $$$$ \\ $$$${since}\:{any}\:{n}\geqslant\mathrm{1}\:{fulfills}\:{this},\:{we}\:{have} \\ $$$${infinitely}\:{many}\:{such}\:{GP}. \\ $$$$ \\ $$$$\Rightarrow\:{Answer}\:\left({d}\right)\:{is}\:{correct}. \\ $$$$ \\ $$$${Examples} \\ $$$${n}=\mathrm{1}: \\ $$$$\mathrm{8},\mathrm{12},\mathrm{18},\mathrm{27}..... \\ $$$$ \\ $$$${n}=\mathrm{2}: \\ $$$$\mathrm{8},\mathrm{8}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ,\mathrm{12},\mathrm{12}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ,\mathrm{18},\mathrm{18}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ,\mathrm{27}.... \\ $$$$ \\ $$$${n}=\mathrm{3}: \\ $$$$\mathrm{8},\mathrm{8}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ,\mathrm{8}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} ,\mathrm{12},\mathrm{12}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ,\mathrm{12}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} ,\mathrm{18},\mathrm{18}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ,\mathrm{18}×\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} ,\mathrm{27}.... \\ $$
