Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 1231 by Rasheed Soomro last updated on 16/Jul/15

i^2 =i.i=(√(−1)).(√(−1))=(√(−1×−1))=(√1)=1??? i^2 =1⇒−1=1??? Resolve the contradiction.

$${i}^{\mathrm{2}} ={i}.{i}=\sqrt{−\mathrm{1}}.\sqrt{−\mathrm{1}}=\sqrt{−\mathrm{1}×−\mathrm{1}}=\sqrt{\mathrm{1}}=\mathrm{1}??? \\ $$$${i}^{\mathrm{2}} =\mathrm{1}\Rightarrow−\mathrm{1}=\mathrm{1}???\: \\ $$$${Resolve}\:{the}\:{contradiction}. \\ $$

Commented by prakash jain last updated on 17/Jul/15

n^(th) root of number gives n different values. Number y x^n =y⇒x^n −y=0 You will get n solutions. We csnnot equate one solution to another solution to create a contradiction. x^2 =(−1)^2 ⇒(x+1)(x−1)=0 x=1 or −1 On LHS you are taking one solution and on RHS you are taking another solution. x^n =y^n ⇏x=y

$${n}^{{th}} \:\mathrm{root}\:\mathrm{of}\:\mathrm{number}\:\mathrm{gives}\:{n}\:\mathrm{different}\:\mathrm{values}. \\ $$$$\mathrm{Number}\:{y} \\ $$$${x}^{{n}} ={y}\Rightarrow{x}^{{n}} −{y}=\mathrm{0} \\ $$$$\mathrm{You}\:\mathrm{will}\:\mathrm{get}\:{n}\:\mathrm{solutions}. \\ $$$$\mathrm{We}\:\mathrm{csnnot}\:\mathrm{equate}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{another} \\ $$$$\mathrm{solution}\:\mathrm{to}\:\mathrm{create}\:\mathrm{a}\:\mathrm{contradiction}. \\ $$$${x}^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{2}} \Rightarrow\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{1}\:{or}\:−\mathrm{1} \\ $$$$\mathrm{On}\:\mathrm{LHS}\:\mathrm{you}\:\mathrm{are}\:\mathrm{taking}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{and} \\ $$$$\mathrm{on}\:\mathrm{RHS}\:\mathrm{you}\:\mathrm{are}\:\mathrm{taking}\:\mathrm{another}\:\mathrm{solution}. \\ $$$${x}^{{n}} ={y}^{{n}} \nRightarrow{x}={y} \\ $$

Commented by Rasheed Ahmad last updated on 31/Jul/15

Dear Prakash Pl connect your comment more directly to the question.

$${Dear}\:{Prakash} \\ $$$${Pl}\:{connect}\:{your}\:{comment}\:{more}\: \\ $$$${directly}\:{to}\:{the}\:{question}. \\ $$

Answered by 123456 last updated on 17/Jul/15

the problem is that because of nature (√(xy))=(√x)(√y) hold for x>0∧y>0 (√x)=y⇒x=y^2 the (√ ) is the positive choise of sign since (±1)^2 =1 ((√1)=+1 but not −1) then manipulating (√ ) are to be made with caution in C(even into R)

$$ \\ $$$$\mathrm{the}\:\mathrm{problem}\:\mathrm{is}\:\mathrm{that}\:\mathrm{because}\:\mathrm{of}\:\mathrm{nature} \\ $$$$\sqrt{{xy}}=\sqrt{{x}}\sqrt{{y}}\:\mathrm{hold}\:\mathrm{for}\:{x}>\mathrm{0}\wedge{y}>\mathrm{0} \\ $$$$\sqrt{{x}}={y}\Rightarrow{x}={y}^{\mathrm{2}} \\ $$$$\mathrm{the}\:\sqrt{\:}\:\mathrm{is}\:\mathrm{the}\:\mathrm{positive}\:\mathrm{choise}\:\mathrm{of}\:\mathrm{sign}\:\mathrm{since} \\ $$$$\left(\pm\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1}\:\left(\sqrt{\mathrm{1}}=+\mathrm{1}\:\mathrm{but}\:\mathrm{not}\:−\mathrm{1}\right) \\ $$$$\mathrm{then}\:\mathrm{manipulating}\:\sqrt{\:}\:\mathrm{are}\:\mathrm{to}\:\mathrm{be}\:\mathrm{made} \\ $$$$\mathrm{with}\:\mathrm{caution}\:\mathrm{in}\:\mathbb{C}\left(\mathrm{even}\:\mathrm{into}\:\mathbb{R}\right) \\ $$

Commented by 123456 last updated on 17/Jul/15

its a bit complex to talk about it, for exaple (√1)=±1 (√1)=(√(−1×−1))=(√(−1))×(√(−1))=±^1 i×±^2 i=±i^2 =±1 its much sensible to choose of branch multivariable functions are complex look that for z=x+yi e^z =e^(x+yi) =e^x (cos y+isin y) and remember that sin y=sin(y+2πk),k∈Z then for n∈N^∗ ln z=ln ∣z∣+(arg z+2πk)i z^(1/n) =e^((ln z)/n) =e^((ln ∣z∣)/n) e^((((arg z)/n)+((2π)/n)k)i) =^n (√(∣z∣))[cos (((arg z)/n)+((2π)/n)k)+isin (((arg z)/n)+((2π)/n)k)] where you can see that the branch choose is very importantuy with it you get n possible n roots to a number try to read some book ate multivariable valued function, it think it will help you. :)

$$\mathrm{its}\:\mathrm{a}\:\mathrm{bit}\:\mathrm{complex}\:\mathrm{to}\:\mathrm{talk}\:\mathrm{about}\:\mathrm{it},\:\mathrm{for}\:\mathrm{exaple} \\ $$$$\sqrt{\mathrm{1}}=\pm\mathrm{1} \\ $$$$\sqrt{\mathrm{1}}=\sqrt{−\mathrm{1}×−\mathrm{1}}=\sqrt{−\mathrm{1}}×\sqrt{−\mathrm{1}}=\overset{\mathrm{1}} {\pm}{i}×\overset{\mathrm{2}} {\pm}{i}=\pm{i}^{\mathrm{2}} =\pm\mathrm{1} \\ $$$$\mathrm{its}\:\mathrm{much}\:\mathrm{sensible}\:\mathrm{to}\:\mathrm{choose}\:\mathrm{of}\:\mathrm{branch} \\ $$$$\mathrm{multivariable}\:\mathrm{functions}\:\mathrm{are}\:\mathrm{complex} \\ $$$$\mathrm{look}\:\mathrm{that}\:\mathrm{for}\:{z}={x}+{yi} \\ $$$${e}^{{z}} ={e}^{{x}+{yi}} ={e}^{{x}} \left(\mathrm{cos}\:{y}+{i}\mathrm{sin}\:{y}\right) \\ $$$$\mathrm{and}\:\mathrm{remember}\:\mathrm{that}\:\mathrm{sin}\:{y}=\mathrm{sin}\left({y}+\mathrm{2}\pi{k}\right),{k}\in\mathbb{Z} \\ $$$$\mathrm{then}\:\mathrm{for}\:{n}\in\mathbb{N}^{\ast} \\ $$$$\mathrm{ln}\:{z}=\mathrm{ln}\:\mid{z}\mid+\left(\mathrm{arg}\:{z}+\mathrm{2}\pi{k}\right){i} \\ $$$${z}^{\frac{\mathrm{1}}{{n}}} ={e}^{\frac{\mathrm{ln}\:{z}}{{n}}} ={e}^{\frac{\mathrm{ln}\:\mid{z}\mid}{{n}}} {e}^{\left(\frac{\mathrm{arg}\:{z}}{{n}}+\frac{\mathrm{2}\pi}{{n}}{k}\right){i}} \\ $$$$\:\:\:\:\:\:=^{{n}} \sqrt{\mid{z}\mid}\left[\mathrm{cos}\:\left(\frac{\mathrm{arg}\:{z}}{{n}}+\frac{\mathrm{2}\pi}{{n}}{k}\right)+{i}\mathrm{sin}\:\left(\frac{\mathrm{arg}\:{z}}{{n}}+\frac{\mathrm{2}\pi}{{n}}{k}\right)\right] \\ $$$$\mathrm{where}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{that}\:\mathrm{the}\:\mathrm{branch}\:\mathrm{choose}\:\mathrm{is}\:\mathrm{very}\:\mathrm{importantuy} \\ $$$$\mathrm{with}\:\mathrm{it}\:\mathrm{you}\:\mathrm{get}\:{n}\:\mathrm{possible}\:{n}\:\mathrm{roots}\:\mathrm{to}\:\mathrm{a}\:\mathrm{number} \\ $$$$\left.\mathrm{try}\:\mathrm{to}\:\mathrm{read}\:\mathrm{some}\:\mathrm{book}\:\mathrm{ate}\:\mathrm{multivariable}\:\mathrm{valued}\:\mathrm{function},\:\mathrm{it}\:\mathrm{think}\:\mathrm{it}\:\mathrm{will}\:\mathrm{help}\:\mathrm{you}.\::\right) \\ $$

Commented by Rasheed Ahmad last updated on 17/Jul/15

You are very right. The rule (√x).(√y)=(√(x.y)) is restricted to avoide such contradictions. It should be used only when x>0 and y>0. But then how can we change (√(−4 )) into iota form?Normally the process is: (√(−4))=(√(4×−1))=(√4)×(√(−1))=2i Here we use the rule even −1<0. Why?

$${You}\:{are}\:{very}\:{right}.\:{The}\:{rule} \\ $$$$\sqrt{{x}}.\sqrt{{y}}=\sqrt{{x}.{y}}\:{is}\:{restricted}\:{to}\:{avoide} \\ $$$${such}\:{contradictions}. \\ $$$${It}\:{should}\:{be}\:{used}\:{only}\:{when}\:{x}>\mathrm{0} \\ $$$${and}\:{y}>\mathrm{0}. \\ $$$${But}\:{then}\:{how}\:{can}\:{we}\:{change}\:\sqrt{−\mathrm{4}\:} \\ $$$${into}\:{iota}\:{form}?{Normally}\:{the}\: \\ $$$${process}\:{is}: \\ $$$$\sqrt{−\mathrm{4}}=\sqrt{\mathrm{4}×−\mathrm{1}}=\sqrt{\mathrm{4}}×\sqrt{−\mathrm{1}}=\mathrm{2}{i} \\ $$$${Here}\:{we}\:{use}\:{the}\:{rule}\:{even}\:−\mathrm{1}<\mathrm{0}. \\ $$$${Why}? \\ $$

Commented by Rasheed Ahmad last updated on 17/Jul/15

The symbol (√( )) means positive sqr root as you mentioned this in your answer.But in your comment you have used it for + and negative root both. Whereas for both roots ±(√( )) is used.

$${The}\:{symbol}\:\sqrt{\:\:\:}\:{means}\:{positive}\:{sqr} \\ $$$${root}\:{as}\:{you}\:{mentioned}\:{this}\:{in}\:{your} \\ $$$${answer}.{But}\:{in}\:{your}\:{comment}\: \\ $$$${you}\:{have}\:{used}\:{it}\:{for}\:+\:{and}\:{negative} \\ $$$${root}\:{both}.\:{Whereas}\:{for}\:{both}\:{roots} \\ $$$$\pm\sqrt{\:\:\:\:}\:{is}\:{used}. \\ $$

Answered by e.nolley@ieee.org last updated on 17/Jul/15

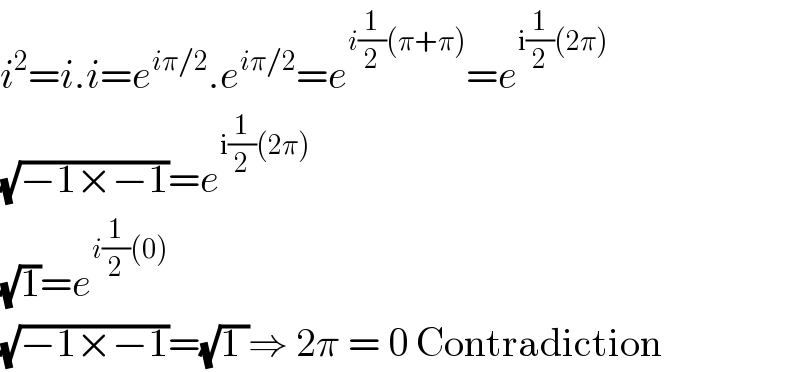
i^2 =i.i=e^(iπ/2) .e^(iπ/2) =e^(i(1/2)(π+π)) =e^(i(1/2)(2π)) (√(−1×−1))=e^(i(1/2)(2π)) (√1)=e^(i(1/2)(0)) (√(−1×−1))=(√(1 ))⇒ 2π = 0 Contradiction

$${i}^{\mathrm{2}} ={i}.{i}={e}^{{i}\pi/\mathrm{2}} .{e}^{{i}\pi/\mathrm{2}} ={e}^{{i}\frac{\mathrm{1}}{\mathrm{2}}\left(\pi+\pi\right)} ={e}^{\mathrm{i}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\pi\right)} \\ $$$$\sqrt{−\mathrm{1}×−\mathrm{1}}={e}^{\mathrm{i}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\pi\right)} \\ $$$$\sqrt{\mathrm{1}}={e}^{{i}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}\right)} \\ $$$$\sqrt{−\mathrm{1}×−\mathrm{1}}=\sqrt{\mathrm{1}\:}\Rightarrow\:\mathrm{2}\pi\:=\:\mathrm{0}\:\mathrm{Contradiction} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com