Is there any solution(s)?? { ((36x^2 y−27y^3 =8)),((4x^3 −27xy^2 =4)) :} please....


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 123114 by nimnim last updated on 23/Nov/20
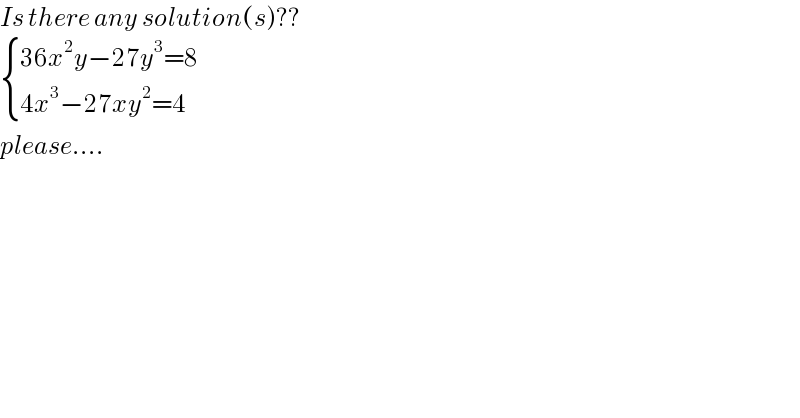
$Is there any solution(s)?? { ((36x^2 y−27y^3 =8)),((4x^3 −27xy^2 =4)) :} please....$
$I s t h e r e a n y s o l u t i o n (s) ? ?$ ${\begin{cases} 36 x^{2} y - 27 y^{3} = 8 \\ 4 x^{3} - 27 {x y}^{2} = 4 \end{cases}$ $p l e a s e . . . .$
Commented by benjo_mathlover last updated on 23/Nov/20
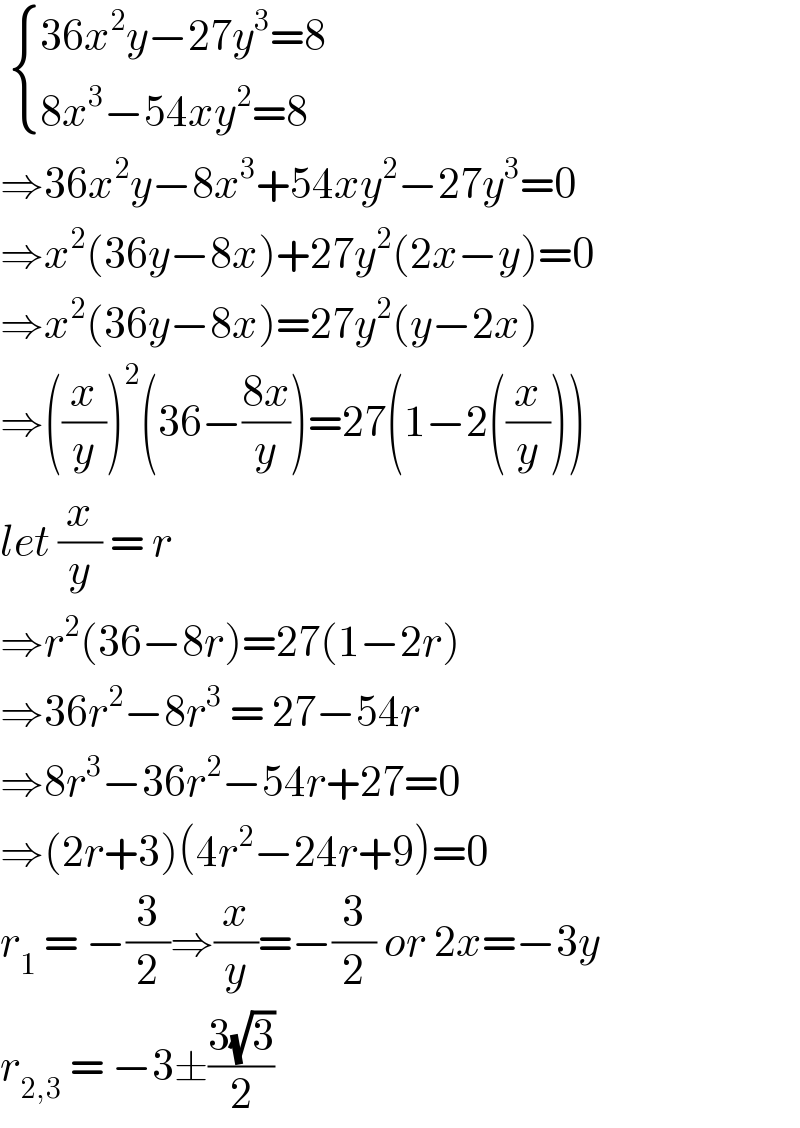
${ ((36x^2 y−27y^3 =8)),((8x^3 −54xy^2 =8)) :} ⇒36x^2 y−8x^3 +54xy^2 −27y^3 =0 ⇒x^2 (36y−8x)+27y^2 (2x−y)=0 ⇒x^2 (36y−8x)=27y^2 (y−2x) ⇒((x/y))^2 (36−((8x)/y))=27(1−2((x/y))) let (x/y) = r ⇒r^2 (36−8r)=27(1−2r) ⇒36r^2 −8r^3 = 27−54r ⇒8r^3 −36r^2 −54r+27=0 ⇒(2r+3)(4r^2 −24r+9)=0 r_1 = −(3/2)⇒(x/y)=−(3/2) or 2x=−3y r_(2,3) = −3±((3(√3))/2)$
${\begin{cases} 36 x^{2} y - 27 y^{3} = 8 \\ 8 x^{3} - 54 {x y}^{2} = 8 \end{cases}$ $\Rightarrow 36 x^{2} y - 8 x^{3} + 54 {x y}^{2} - 27 y^{3} = 0$ $\Rightarrow x^{2} (36 y - 8 x) + 27 y^{2} (2 x - y) = 0$ $\Rightarrow x^{2} (36 y - 8 x) = 27 y^{2} (y - 2 x)$ $\Rightarrow {(\frac{x}{y})}^{2} (36 - \frac{8 x}{y}) = 27 (1 - 2 (\frac{x}{y}))$ $l e t \frac{x}{y} = r$ $\Rightarrow r^{2} (36 - 8 r) = 27 (1 - 2 r)$ $\Rightarrow 36 r^{2} - 8 r^{3} = 27 - 54 r$ $\Rightarrow 8 r^{3} - 36 r^{2} - 54 r + 27 = 0$ $\Rightarrow (2 r + 3) (4 r^{2} - 24 r + 9) = 0$ $r_{1} = - \frac{3}{2} \Rightarrow \frac{x}{y} = - \frac{3}{2} o r 2 x = - 3 y$ $r_{2, 3} = - 3 \pm \frac{3 \sqrt{3}}{2}$
Commented by nimnim last updated on 23/Nov/20

$T h a n k y o u S i r .$
	Answered by mindispower last updated on 23/Nov/20
	$⇔multiplie (1).i { ((36ix^2 y−27iy^3 =8i..(1))),((8x^3 −54xy^2 =8....(2))) :} and Eq 2 ∗2 (1)+(2)⇒−27iy^3 +8x^3 −54xy^2 +36ix^2 y=16 ⇔(3iy)^3 +(2x)^3 +3(3iy)^2 2+3(3iy)(2x)^2 =8(i+1) ⇔(3iy+2x)^3 =8(√2)e^(((iπ)/4)+i2kπ) ....x,y∈R this is suffisant to solve it if x,y∈C (1)∗−i+...(2)∗2 ⇒(−3iy)^3 +3(−3iy)(2x)^2 +(2x)^3 +3(−3iy)^2 .2x=−8i+8 ⇒(2x−3iy)^3 =8(1−i)=8(√2)e^(−((iπ)/4)+2k_1 π) ,k_1 ∈{0,1,2} ⇔ { ((2x−3iy=8(√2)e^(−i(π/(12))+2((ikπ)/3)) )),((2x+3iy=8(√2)e^(i(π/(12))+2((k_1 π)/3)) )) :} solve and theck evry solution because We used ⇒$
	$\Leftrightarrow m u l t i p l i e (1) . i {\begin{cases} 36 {i x}^{2} y - 27 {i y}^{3} = 8 i . . (1) \\ 8 x^{3} - 54 {x y}^{2} = 8 . . . . (2) \end{cases}$ $a n d E q 2 * 2$ $(1) + (2) \Rightarrow - 27 {i y}^{3} + 8 x^{3} - 54 {x y}^{2} + 36 {i x}^{2} y = 16$ $\Leftrightarrow {(3 i y)}^{3} + {(2 x)}^{3} + 3 {(3 i y)}^{2} 2 + 3 (3 i y) {(2 x)}^{2} = 8 (i + 1)$ $\Leftrightarrow {(3 i y + 2 x)}^{3} = 8 \sqrt{2} e^{\frac{i π}{4} + i 2 k π} . . . . x, y \in R$ $t h i s i s s u f f i s a n t t o s o l v e i t$ $i f x, y \in C$ $(1) * - i + . . . (2) * 2$ $\Rightarrow {(- 3 i y)}^{3} + 3 (- 3 i y) {(2 x)}^{2} + {(2 x)}^{3} + 3 {(- 3 i y)}^{2} . 2 x = - 8 i + 8$ $\Rightarrow {(2 x - 3 i y)}^{3} = 8 (1 - i) = 8 \sqrt{2} e^{- \frac{i π}{4} + 2 k_{1} π}, k_{1} \in {0, 1, 2}$ $\Leftrightarrow {\begin{cases} 2 x - 3 i y = 8 \sqrt{2} e^{- i \frac{π}{12} + 2 \frac{i k π}{3}} \\ 2 x + 3 i y = 8 \sqrt{2} e^{i \frac{π}{12} + 2 \frac{k_{1} π}{3}} \end{cases}$ $s o l v e a n d t h e c k e v r y s o l u t i o n b e c a u s e W e$ $u s e d \Rightarrow$
	Commented by nimnim last updated on 23/Nov/20

	$T h a n k y o u S i r .$
	Answered by MJS_new last updated on 23/Nov/20

	$the easy path$ $36 x^{2} y - 27 y^{3} = 8$ $4 x^{3} - 27 {x y}^{2} = 4$ $let y = p x$ $36 {p x}^{3} - 27 p^{3} x^{3} = 8 \Leftrightarrow x^{3} = \frac{8}{36 p - 27 p^{3}}$ $4 x^{3} - 27 p^{2} x^{3} = 4 \Leftrightarrow x^{3} = \frac{4}{4 - 27 p^{2}}$ $\Rightarrow$ $36 p - 27 p^{3} = 8 - 54 p^{2}$ $p^{3} - 2 p^{2} - \frac{4}{3} p + \frac{8}{27} = 0$ $p_{1} = - \frac{2}{3}$ $p_{2} = \frac{4 - 2 \sqrt{3}}{3}$ $p_{3} = \frac{4 + 2 \sqrt{3}}{3}$ $\Rightarrow$ $x_{1} = - \frac{\sqrt[3]{4}}{2} \land y_{1} = \frac{\sqrt[3]{4}}{3}$ $x_{2} = \frac{\sqrt[3]{4}}{4} (1 + \sqrt{3}) \land y_{2} = \frac{\sqrt[3]{4}}{6} (- 1 + \sqrt{3})$ $x_{3} = - \frac{\sqrt[3]{4}}{4} (- 1 + \sqrt{3}) \land y_{3} = - \frac{\sqrt[3]{4}}{6} (1 + \sqrt{3})$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum