Question Number 123326 by Dwaipayan Shikari last updated on 24/Nov/20
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} +{n}^{\mathrm{2}} +{n}+\mathrm{1}} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Nov/20
$${I}\:{have}\:{found}\:\frac{\gamma−\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}{i}}\left(\left(\mathrm{1}−{i}\right)\psi\left(\mathrm{1}−{i}\right)−\left(\mathrm{1}+{i}\right)\psi\left({i}\right)−\mathrm{1}−{i}\right) \\ $$
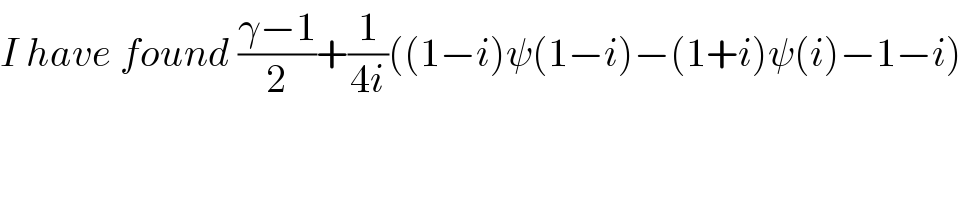
Answered by mnjuly1970 last updated on 25/Nov/20
![=Σ(1/((n^2 +1)(n+1)))=Σ_(n=1) ^∞ (1/((n−i)(n+i)(n+1))) =(1/(2i))Σ_(n=1) ^∞ [(1/((n−i)(n+1))) −(1/((n+i)(n+1)))] (1/(2i))Σ_(n=1) ^∞ ((1/((n−i)(n+1))))−(1/(2i))Σ_(n=1) ^∞ ((1/((n+i)(n+1)))) (1/(2i(1+i))){Σ_(n=1) ^∞ (1/(n−i)) −(1/(n+1))}−(1/(2i(1−i))){Σ_(n=1) ^∞ (1/(n+i))−(1/(n+1))} =(1/(2i(1+i)))(ψ(2)−ψ(1−i))−(1/(2i(1−i)))(ψ(2)−ψ(1+i)) =[(1/(2i(1+i)))−(1/(2i(1−i)))]ψ(2)+(1/(2i(1−i)))ψ(1+i)−(1/(2i(1+i)))ψ(1−i) =((−2i)/(2i(1+1)))ψ(2)+{(1/(2i))[((ψ(1+i))/(1−i))−((ψ(1−i))/(1+i))]} =((−1)/2)(1−γ)+{(1/(4i))[(1+i)ψ(1+i)−(1−i)ψ(1−i)]}=A =(1/2)(γ−1)+A^? ✓](Q123366.png)
$$=\Sigma\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +\mathrm{1}\right)\left({n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−{i}\right)\left({n}+{i}\right)\left({n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\left({n}−{i}\right)\left({n}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\left({n}+{i}\right)\left({n}+\mathrm{1}\right)}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left({n}−{i}\right)\left({n}+\mathrm{1}\right)}\right)−\frac{\mathrm{1}}{\mathrm{2}{i}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\left({n}+{i}\right)\left({n}+\mathrm{1}\right)}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}+{i}\right)}\left\{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}−{i}}\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right\}−\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}−{i}\right)}\left\{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+{i}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}+{i}\right)}\left(\psi\left(\mathrm{2}\right)−\psi\left(\mathrm{1}−{i}\right)\right)−\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}−{i}\right)}\left(\psi\left(\mathrm{2}\right)−\psi\left(\mathrm{1}+{i}\right)\right) \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}+{i}\right)}−\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}−{i}\right)}\right]\psi\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}−{i}\right)}\psi\left(\mathrm{1}+{i}\right)−\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}+{i}\right)}\psi\left(\mathrm{1}−{i}\right) \\ $$$$=\frac{−\mathrm{2}{i}}{\mathrm{2}{i}\left(\mathrm{1}+\mathrm{1}\right)}\psi\left(\mathrm{2}\right)+\left\{\frac{\mathrm{1}}{\mathrm{2}{i}}\left[\frac{\psi\left(\mathrm{1}+{i}\right)}{\mathrm{1}−{i}}−\frac{\psi\left(\mathrm{1}−{i}\right)}{\mathrm{1}+{i}}\right]\right\} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\gamma\right)+\left\{\frac{\mathrm{1}}{\mathrm{4}{i}}\left[\left(\mathrm{1}+{i}\right)\psi\left(\mathrm{1}+{i}\right)−\left(\mathrm{1}−{i}\right)\psi\left(\mathrm{1}−{i}\right)\right]\right\}={A} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\gamma−\mathrm{1}\right)+\overset{?} {{A}}\:\checkmark \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 25/Nov/20
$${Great}!\:{thanking}\:{you}\:{sir} \\ $$
Commented by mnjuly1970 last updated on 25/Nov/20
$${peace}\:{be}\:{upon}\:{you} \\ $$$${sir}\:{payan}. \\ $$
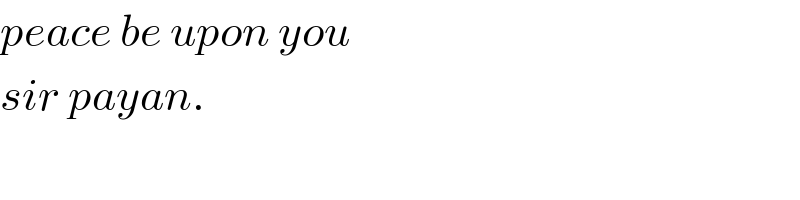
Commented by mnjuly1970 last updated on 25/Nov/20
Commented by mnjuly1970 last updated on 25/Nov/20
