find the maximum and minimum values of 2cos2x−cos4x in the range 0<x<π. sketch the curve


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 123337 by aurpeyz last updated on 25/Nov/20

$f i n d t h e m a x i m u m a n d m i n i m u m$ $v a l u e s o f 2 c o s 2 x - c o s 4 x i n t h e r a n g e$ $0 < x < π . s k e t c h t h e c u r v e$
Commented bybemath last updated on 25/Nov/20

$m a x = 1.5; m i n = - 3$ $r a n g e \Rightarrow - 3 ⩽ y ⩽ 1.5$
Commented bybemath last updated on 25/Nov/20

Commented byaurpeyz last updated on 25/Nov/20

$t h a n k s$
Commented byaurpeyz last updated on 25/Nov/20

$p l s e x p l a i n h o w y o u g o t m i n = - 3 .$ $i t r i e d s o h a r d b u t c o u l d n t$
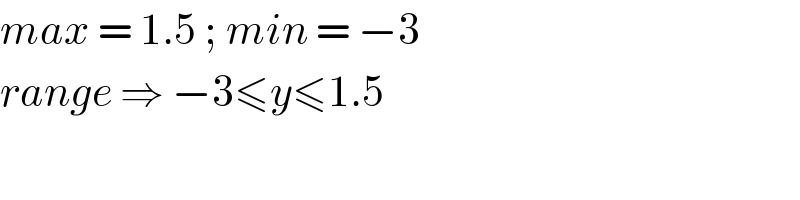
Commented bybemath last updated on 25/Nov/20
$let ∅(x)=2cos 2x−cos 4x ∅(x)=2cos 2x−(2cos^2 2x−1) ∅(x)=−2cos^2 2x+2cos 2x+1 ∅(x) = −2(cos^2 2x−cos 2x)+1 ∅(x)=−2[(cos 2x−(1/2))^2 −(1/4)]+1 ∅(x)=−2(cos 2x−(1/2))^2 +(3/2) → { ((max when cos 2x=(1/2))),((min when cos 2x=−1)) :}$
$l e t \emptyset (x) = 2 \cos 2 x - \cos 4 x$ $\emptyset (x) = 2 \cos 2 x - (2 \cos^{2} 2 x - 1)$ $\emptyset (x) = - 2 \cos^{2} 2 x + 2 \cos 2 x + 1$ $\emptyset (x) = - 2 (\cos^{2} 2 x - \cos 2 x) + 1$ $\emptyset (x) = - 2 [{(\cos 2 x - \frac{1}{2})}^{2} - \frac{1}{4}] + 1$ $\emptyset (x) = - 2 {(\cos 2 x - \frac{1}{2})}^{2} + \frac{3}{2}$ $\to {\begin{cases} m a x w h e n \cos 2 x = \frac{1}{2} \\ m i n w h e n \cos 2 x = - 1 \end{cases}$
Commented byMJS_new last updated on 25/Nov/20
$cos 2x =−1+2cos^2 x cos 4x =−1+2cos^2 2x = =−1+2(−1+2cos^2 x)^2 = =1−8cos^2 x +8cos^4 x ⇒2cos 2x −cos 4x = =−3+12cos^2 x −8cos^4 x =f(x) we can always use t=tan (x/2) ⇔ x=2arctan t ⇒ sin x =((2t)/(t^2 +1))∧cos x =−((t^2 −1)/(t^2 +1)) ⇒ −3+12cos^2 x −8cos^4 x = =((t^8 +20t^6 −90t^4 +20t^2 +1)/((t^2 +1)^4 ))=g(t) (dg/dt)=0 −32((t(t^6 −15t^4 +15t^2 −1))/((t^2 +1)^5 ))=0 t(t^6 −15t^4 +15t^2 −1)=0 t_1 =0 t^6 −15t^4 +15t^2 −1=0 trying factors of −1 ⇒ t_(2, 3) =±1 t^4 −14t^2 +1=0 ⇒ t^2 =7±4(√3) ⇒ t=±(√(7±4(√3)))=±(2±(√3)) now we have t∈{−2−(√3), −1, −2+(√3), 0, 2−(√3), 1, 2+(√3)} now t=tan (x/2) ⇒ x=2nπ+2arctan t for 0<x<π we get (x=0∨x=π ⇒ f(x)=1) x=(π/6) ⇒ f(x)=(3/2) x=(π/2) ⇒ f(x)=−3 x=((5π)/6) ⇒ f(x)=(3/2) ⇒ minimum is −3 and maximum is (3/2)$
$\cos 2 x = - 1 + {2 \cos}^{2} x$ $\cos 4 x = - 1 + {2 \cos}^{2} 2 x =$ $= - 1 + 2 {(- 1 + {2 \cos}^{2} x)}^{2} =$ $= 1 - {8 \cos}^{2} x + {8 \cos}^{4} x$ $\Rightarrow 2 \cos 2 x - \cos 4 x =$ $= - 3 + {12 \cos}^{2} x - {8 \cos}^{4} x = f (x)$ $we can always use$ $t = \tan \frac{x}{2} \Leftrightarrow x = 2 \arctan t$ $\Rightarrow \sin x = \frac{2 t}{t^{2} + 1} \land \cos x = - \frac{t^{2} - 1}{t^{2} + 1}$ $\Rightarrow - 3 + {12 \cos}^{2} x - {8 \cos}^{4} x =$ $= \frac{t^{8} + 20 t^{6} - 90 t^{4} + 20 t^{2} + 1}{{(t^{2} + 1)}^{4}} = g (t)$ $\frac{d g}{d t} = 0$ $- 32 \frac{t (t^{6} - 15 t^{4} + 15 t^{2} - 1)}{{(t^{2} + 1)}^{5}} = 0$ $t (t^{6} - 15 t^{4} + 15 t^{2} - 1) = 0$ $t_{1} = 0$ $t^{6} - 15 t^{4} + 15 t^{2} - 1 = 0$ $trying factors of - 1 \Rightarrow t_{2, 3} = \pm 1$ $t^{4} - 14 t^{2} + 1 = 0$ $\Rightarrow t^{2} = 7 \pm 4 \sqrt{3}$ $\Rightarrow t = \pm \sqrt{7 \pm 4 \sqrt{3}} = \pm (2 \pm \sqrt{3})$ $now we have$ $t \in {- 2 - \sqrt{3}, - 1, - 2 + \sqrt{3}, 0, 2 - \sqrt{3}, 1, 2 + \sqrt{3}}$ $now t = \tan \frac{x}{2} \Rightarrow x = 2 n π + 2 \arctan t$ $for 0 < x < π we get$ $(x = 0 \lor x = π \Rightarrow f (x) = 1)$ $x = \frac{π}{6} \Rightarrow f (x) = \frac{3}{2}$ $x = \frac{π}{2} \Rightarrow f (x) = - 3$ $x = \frac{5 π}{6} \Rightarrow f (x) = \frac{3}{2}$ $\Rightarrow minimum is - 3 and maximum is \frac{3}{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum