Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 123552 by Lordose last updated on 26/Nov/20

$${\int }_0^{\frac{\pi }{4}}{\tan }^{\mathrm{n}}\left(\mathrm{x}\right)\mathrm{dx}$$

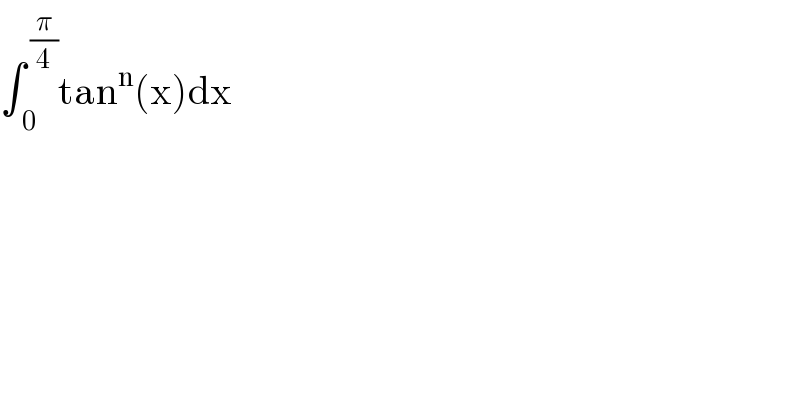
Answered by Adeleke last updated on 26/Nov/20

Answered by TANMAY PANACEA last updated on 26/Nov/20

$$I_n={\int }_0^{\frac{\pi }{4}}{tan}^{n-2}x({sec}^{2}x-1)dx$$$$={\int }_0^{\frac{\pi }{4}}{tan}^{n-2}x\times d\left(tanx\right)-I_{n-2}$$$$=\mid \frac{{tan}^{n-1}x}{n-1}{\mid }_0^{\frac{\pi }{4}}-I_{n-2}$$$$=\frac{1}{n-1}-I_{n-2}$$$$I_n=\frac{1}{n-1}-I_{n-2}$$

Commented by peter frank last updated on 26/Nov/20

$$\mathrm{thank}\mathrm{you}$$

Answered by Dwaipayan Shikari last updated on 26/Nov/20

$$Ifitwas{\int }_0^{\frac{\pi }{2}}{tan}^{n}xdx$$$$thenwecangetaclosedform$$$${\int }_0^{\frac{\pi }{2}}{sin}^{n}x{cos}^{-n}xdx$$$$=\frac{1}{2}{\int }_0^1{t}^{\frac{n}{2}-\frac{1}{2}}{(1-t)}^{\frac{-n}{2}-\frac{1}{2}}dt{sin}^{2}x=t$$$$=\frac{1}{2}\frac{\mathrm{\Gamma }(\frac{n}{2}+\frac{1}{2})\mathrm{\Gamma }(\frac{1}{2}-\frac{n}{2})}{\mathrm{\Gamma }\left(1\right)}=\frac{\pi }{2sin(\frac{n\pi }{2}+\frac{\pi }{2})}$$$${\int }_0^{\frac{\pi }{4}}{tan}^{p}xdx={\int }_0^1\frac{t^p}{t^2+1}dt$$$$={\int }_0^1{t}^p\underset{n=0}{\sum ^{\mathrm{\infty }}}{(-1)}^n{t}^{2n}=\underset{n=0}{\sum ^{\mathrm{\infty }}}{(-1)}^n{\int }_0^1{t}^{2n+p}dt=\underset{n=0}{\sum ^{\mathrm{\infty }}}{(-1)}^n\frac{1}{2n+p+1}$$

Answered by mnjuly1970 last updated on 26/Nov/20

$$\mathrm{\Omega }\stackrel{tan\left(x\right)=y}{=}{\int }_0^1\frac{y^{n}dy}{1+y^2}={\int }_0^1\frac{y^n-y^{n+2}}{1-y^4}dy$$$$=\frac{1}{4}{\int }_0^1\frac{t^{\frac{n-3}{4}}-t^{\frac{n-1}{4}}}{1-t}dt$$$$=\frac{1}{4}({\mathrm{H}}_{\frac{n-1}{4}}-{\mathrm{H}}_{\frac{n-3}{4}})$$$$=\frac{1}{4}(\psi (\frac{n}{4}+\frac{3}{4})-\psi (\frac{n}{4}+\frac{1}{4}))✓$$$$$$$$$$$$$$$$$$$$$$

Commented by Dwaipayan Shikari last updated on 26/Nov/20

$${\int }_0^{\frac{\pi }{4}}{tan}^{4}xdx=\frac{1}{4}(\psi (1+\frac{3}{4})-\psi (1+\frac{1}{4}))$$$$=\frac{1}{4}(\psi \left(\frac{3}{4}\right)+\frac{4}{3}-\psi \left(\frac{1}{4}\right)-4)$$$$=\frac{1}{4}(\pi cot\left(\frac{\pi }{4}\right)-\frac{8}{3})=\frac{\pi }{4}-\frac{2}{3}$$

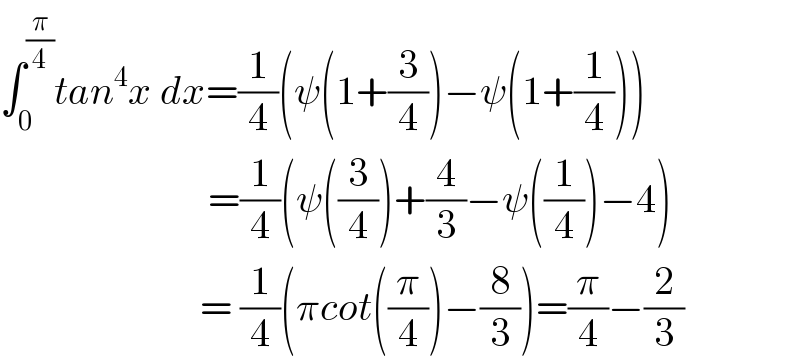
Commented by Lordose last updated on 02/Dec/20

$$\mathrm{Exactly}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com