
Question and Answers Forum
Question Number 123598 by aurpeyz last updated on 26/Nov/20
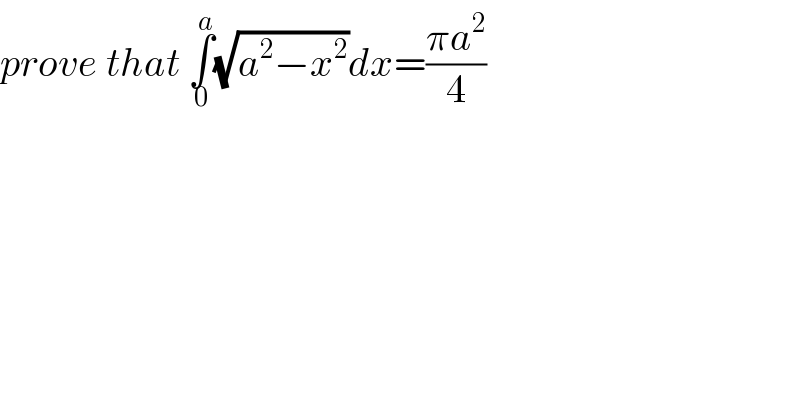
Answered by Dwaipayan Shikari last updated on 26/Nov/20
![∫_0 ^a (√(a^2 −x^2 )) dx x=asinθ ∫_0 ^(π/2) acosθ(√(a^2 −a^2 sin^2 θ)) dθ =a^2 ∫_0 ^(π/2) cos^2 θ =(a^2 /2)∫_0 ^(π/2) 1+cos2θ dx =((πa^2 )/4)+(a^2 /2)∫_0 ^(π/2) cos2θ =((πa^2 )/4)+(a^2 /4)[cos2θ]_0 ^(π/2) =((πa^2 )/4)](Q123602.png)
| ||
Question and Answers Forum | ||
Question Number 123598 by aurpeyz last updated on 26/Nov/20 | ||
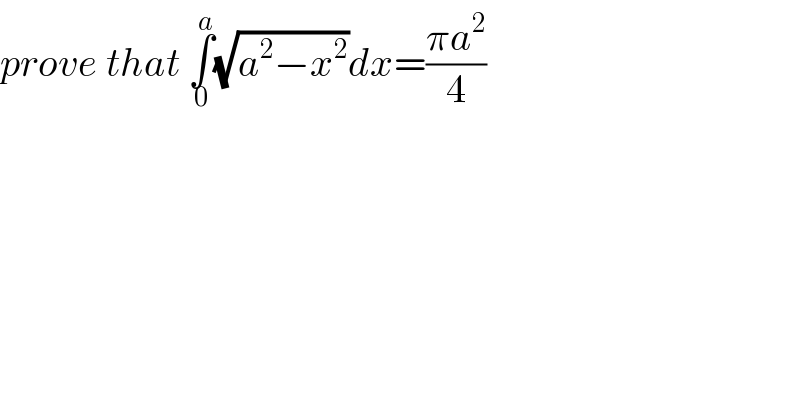 | ||
Answered by Dwaipayan Shikari last updated on 26/Nov/20 | ||
![∫_0 ^a (√(a^2 −x^2 )) dx x=asinθ ∫_0 ^(π/2) acosθ(√(a^2 −a^2 sin^2 θ)) dθ =a^2 ∫_0 ^(π/2) cos^2 θ =(a^2 /2)∫_0 ^(π/2) 1+cos2θ dx =((πa^2 )/4)+(a^2 /2)∫_0 ^(π/2) cos2θ =((πa^2 )/4)+(a^2 /4)[cos2θ]_0 ^(π/2) =((πa^2 )/4)](Q123602.png) | ||
| ||