Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 123676 by mathmax by abdo last updated on 27/Nov/20

$$\mathrm{find}{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\mathrm{x}}\ln (1+{\mathrm{e}}^{2\mathrm{x}})\mathrm{dx}$$

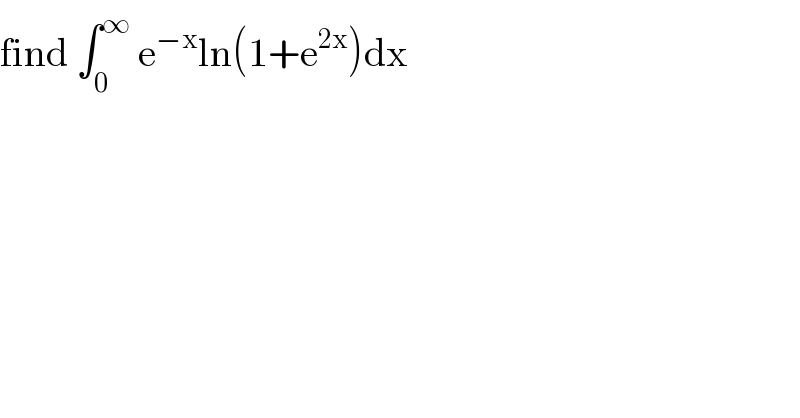
Answered by mnjuly1970 last updated on 27/Nov/20

$$solution$$$$\mathrm{\Omega }={\int }_0^{\mathrm{\infty }}{e}^{-x}ln\left[e^{2x}(1+e^{-2x})\right]dx$$$$=2{\int }_0^{\mathrm{\infty }}{xe}^{-x}dx+{\int }_0^{\mathrm{\infty }}{e}^{-x}ln(1+e^{-2x})dx$$$$=2\mathrm{\Gamma }\left(2\right)+{\int }_0^{\mathrm{\infty }}{e}^{-x}\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^{n-1}{e}^{-2nx}}{n}dx$$$$=2+\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^{n-1}}{n}{\int }_0^{\mathrm{\infty }}{e}^{-x(2n+1)}dx$$$$=2+\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^n}{n}{\left[\frac{e^{-x(2n+1)}}{2n+1}\right]}_0^{\mathrm{\infty }}$$$$=2+\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^{n-1}}{n(2n+1)}=2-[\underset{n=1}{\sum ^{\mathrm{\infty }}}\frac{{(-1)}^n}{n}-\frac{2{(-1)}^n}{2n+1}]$$$$=2+ln\left(2\right)+2[-1+\frac{\pi }{4}]$$$$ln\left(2\right)+\frac{\pi }{2}\approx 2.26$$

Commented by mnjuly1970 last updated on 27/Nov/20

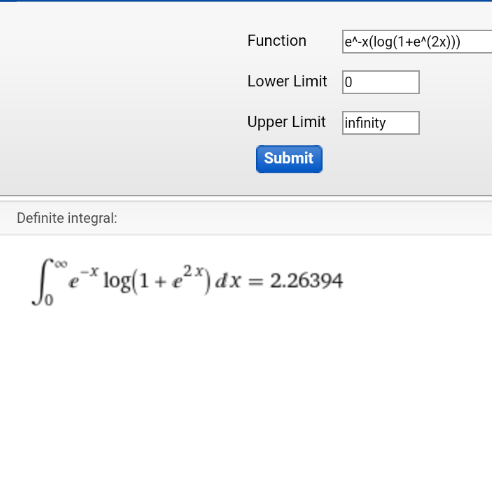
Commented by harckinwunmy last updated on 27/Nov/20

$$\mathrm{can}\mathrm{i}\mathrm{know}\mathrm{the}\mathrm{name}\mathrm{og}$$$$\mathrm{this}\mathrm{app}.\mathrm{thanks}$$

Commented by Dwaipayan Shikari last updated on 27/Nov/20

$$Wolframalpha$$

Commented by Dwaipayan Shikari last updated on 27/Nov/20

https://wolframalpha.com/

Commented by mnjuly1970 last updated on 27/Nov/20

$$thankyoumrpayan$$

Commented by Dwaipayan Shikari last updated on 27/Nov/20

��

Commented by mathmax by abdo last updated on 28/Nov/20

$$\mathrm{thank}\mathrm{you}\mathrm{sir}\mathrm{mn}...$$

Answered by mathmax by abdo last updated on 28/Nov/20

$$\mathrm{I}={\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-\mathrm{x}}\ln (1+{\mathrm{e}}^{2\mathrm{x}})\mathrm{dx}\mathrm{changement}{\mathrm{e}}^{\mathrm{x}}=\mathrm{t}\mathrm{give}$$$$\mathrm{I}={\int }_1^{\mathrm{\infty }}{\mathrm{t}}^{-1}\ln (1+{\mathrm{t}}^2)\frac{\mathrm{dt}}{\mathrm{t}}={\int }_1^{\mathrm{\infty }}\frac{\ln (1+{\mathrm{t}}^2)}{{\mathrm{t}}^2}\mathrm{dt}$$$${=}_{\mathrm{bypsrts}}{[-\frac{1}{\mathrm{t}}\ln (1+{\mathrm{t}}^2)]}_1^{\mathrm{\infty }}+{\int }_1^{\mathrm{\infty }}\frac{1}{\mathrm{t}}\times \frac{2\mathrm{t}}{1+{\mathrm{t}}^2}\mathrm{dt}$$$$=\ln \left(2\right)+2{\int }_1^{\mathrm{\infty }}\frac{\mathrm{dt}}{1+{\mathrm{t}}^2}=\ln \left(2\right)+2{\left[\mathrm{arctant}\right]}_1^{\mathrm{\infty }}$$$$=\ln \left(2\right)+2\{\frac{\pi }{2}-\frac{\pi }{4}\}=\ln \left(2\right)+2\left(\frac{\pi }{4}\right)=\frac{\pi }{2}+\ln \left(2\right)$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com