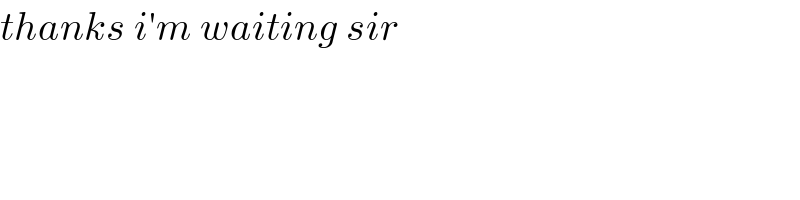Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 123715 by Engr_Jidda last updated on 27/Nov/20

Answered by Dwaipayan Shikari last updated on 27/Nov/20

∫_(−∞) ^∞ (e^(2x) /(e^(3x) +1))dx =2∫_0 ^∞ Σ_(n=1) ^∞ (−1)^(n+1) e^(2x) e^(−3nx) dx =2Σ_(n=1) ^∞ (−1)^(n+1) ∫_0 ^∞ e^(−x(3n−2)) dx x(3n−2)=u =2Σ_(n=1) ^∞ (−1)^(n+1) (1/((3n−2)))∫_0 ^∞ e^(−u) du =2Σ_(n=1) ^∞ (((−1)^(n+1) )/(3n−2))Γ(1) =2Σ_(n=1) ^∞ (((−1)^(n+1) )/(3n−2))=2Σ_(n=0) ^∞ (((−1)^n )/(3n+1))=2Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(3n) =2∫_0 ^1 Σ_(n=0) ^∞ (−1)^n x^(3n) =2∫_0 ^1 (1/(1+x^3 ))dx =2∫_0 ^1 (1/(3(1+x)))+((−(x/3)+(2/3))/(1−x+x^2 ))dx =−(1/3)∫_0 ^1 ((2x−1)/(x^2 −x+1))+∫(1/(x^2 −x+1))dx =−(1/3)[log(x^2 −x+1)]_0 ^1 +∫(1/((x−(1/2))^2 +(((√3)/2))^2 ))dx =[(2/( (√3)))tan^(−1) ((2x−1)/( (√3)))]_0 ^1 =((2π)/( 3(√3)))

$$\int_{−\infty} ^{\infty} \frac{{e}^{\mathrm{2}{x}} }{{e}^{\mathrm{3}{x}} +\mathrm{1}}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{\mathrm{2}{x}} {e}^{−\mathrm{3}{nx}} {dx} \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {e}^{−{x}\left(\mathrm{3}{n}−\mathrm{2}\right)} {dx}\:\:\:\:\:\:\:{x}\left(\mathrm{3}{n}−\mathrm{2}\right)={u} \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{3}{n}−\mathrm{2}\right)}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}} {du} \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{3}{n}−\mathrm{2}}\Gamma\left(\mathrm{1}\right) \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{3}{n}−\mathrm{2}}=\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}{n}+\mathrm{1}}=\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{3}{n}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{3}{n}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+{x}\right)}+\frac{−\frac{{x}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx}\:\:\:\: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}+\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\left[{log}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx} \\ $$$$=\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{2}\pi}{\:\mathrm{3}\sqrt{\mathrm{3}}} \\ $$

Answered by mathmax by abdo last updated on 28/Nov/20

A=∫_(−∞) ^(+∞) (e^(2x) /(e^(3x) +1))dx =∫_(−∞) ^0 (e^(2x) /(e^(3x) +1))dx(→x=−t) +∫_0 ^∞ (e^(2x) /(e^(3x) +1))dx =∫_0 ^∞ (e^(−2t) /(e^(−3t) +1))dt +∫_0 ^∞ (e^(2x) /(e^(3x) +1))dx we have ∫_0 ^∞ (e^(−2x) /(e^(−3x) +1))dx = ∫_0 ^∞ e^(−2x) Σ_(n=0) ^∞ (−1)^n e^(−3nx) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(3n+2)x) dx =_((3n+2)x=u) Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−u) (du/(3n+2)) =Σ_(n=0) ^∞ (((−1)^n )/(3n+2)) ∫_0 ^∞ (e^(2x) /(e^(3x) +1))dx =∫_0 ^∞ (e^(−x) /(1+e^(−3x) ))dx =∫_0 ^∞ e^(−x) Σ_(n=0) ^∞ (−1)^n e^(−3nx) =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(3n+1)x) dx =_((3n+1)x=u) Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−u) (du/(3n+1)) =Σ_(n=0) ^∞ (((−1)^n )/(3n+1)) ⇒A =Σ_(n0) ^∞ (((−1)^n )/(3n+2)) +Σ_(n=0) ^∞ (((−1)^n )/(3n+1)) rest calculus those series...be continued...

$$\mathrm{A}=\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{−\infty} ^{\mathrm{0}} \:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{1}}\mathrm{dx}\left(\rightarrow\mathrm{x}=−\mathrm{t}\right)\:+\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{e}^{\mathrm{3x}} +\mathrm{1}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{2t}} }{\mathrm{e}^{−\mathrm{3t}} \:+\mathrm{1}}\mathrm{dt}\:\:+\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{1}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{2x}} }{\mathrm{e}^{−\mathrm{3x}} \:+\mathrm{1}}\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2x}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{3nx}} \mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{3n}+\mathrm{2}\right)\mathrm{x}} \:\mathrm{dx}\:=_{\left(\mathrm{3n}+\mathrm{2}\right)\mathrm{x}=\mathrm{u}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{u}} \frac{\mathrm{du}}{\mathrm{3n}+\mathrm{2}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{3n}+\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{3x}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{3nx}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{3n}+\mathrm{1}\right)\mathrm{x}} \mathrm{dx}\:=_{\left(\mathrm{3n}+\mathrm{1}\right)\mathrm{x}=\mathrm{u}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{u}} \frac{\mathrm{du}}{\mathrm{3n}+\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{3n}+\mathrm{1}}\:\Rightarrow\mathrm{A}\:=\sum_{\mathrm{n0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{3n}+\mathrm{2}}\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{3n}+\mathrm{1}} \\ $$$$\mathrm{rest}\:\mathrm{calculus}\:\mathrm{those}\:\mathrm{series}...\mathrm{be}\:\mathrm{continued}... \\ $$

Commented by Engr_Jidda last updated on 30/Nov/20

thanks i′m waiting sir

$${thanks}\:{i}'{m}\:{waiting}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com