Question Number 123738 by ajfour last updated on 27/Nov/20
Commented by ajfour last updated on 27/Nov/20
$${Find}\:{minimum}\:{of}\:\:\:\frac{{R}}{{s}}\:. \\ $$$${s}\:{is}\:{the}\:{side}\:{of}\:{the}\:{pink}\:{shaded} \\ $$$${equilateral}\:{triangle}. \\ $$
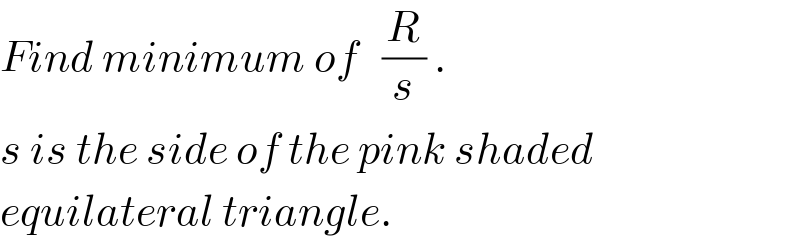
Answered by mr W last updated on 28/Nov/20
Commented by mr W last updated on 28/Nov/20
![AD=((2R sin α)/(sin (α+β))) ∠ABD=α+(π/3) AB=((2R sin α sin (α+β+(π/3)))/(sin (α+β)×sin (α+(π/3)))) s=((2R sin α sin β)/(sin (α+β)×sin (α+(π/3)))) ⇒λ=(s/(2R))=((sin α sin β)/(sin (α+β)×sin (α+(π/3)))) ...(II) AE=2R cos β ED=2R[cos β−((sin α)/(sin (α+β)))] EB=((2R)/(sin (π/3)))[cos β−((sin α)/(sin (α+β)))]sin (α+β+(π/3)) ⇒((EB)/(2R))=(2/( (√3)))[cos β−((sin α)/(sin (α+β)))]sin (α+β+(π/3)) EB^2 =[((2R sin α sin (α+β+(π/3)))/(sin (α+β)×sin (α+(π/3))))]^2 +[2R cos β]^2 −2×((2R sin α sin (α+β+(π/3)))/(sin (α+β)×sin (α+(π/3))))×2R cos β×cos β (((EB)/(2R)))^2 =[((sin α sin (α+β+(π/3)))/(sin (α+β)×sin (α+(π/3))))]^2 +cos^2 β−((2 sin α cos^2 β sin (α+β+(π/3)))/(sin (α+β)×sin (α+(π/3)))) ⇒[((sin α sin (α+β+(π/3)))/(sin (α+(π/3)) sin (α+β)))]^2 +cos^2 β−((2 sin α cos^2 β sin (α+β+(π/3)))/(sin (α+(π/3)) sin (α+β))) =(4/( 3))[cos β sin (α+β)−sin α]^2 [((sin (α+β+(π/3)))/(sin (α+β)))]^2 ...(I) we get from (II) and (I) graphically λ_(max) =(s_(max) /(2R))≈0.1831 at α≈16.5° and β≈24°](Q123783.png)
$${AD}=\frac{\mathrm{2}{R}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)} \\ $$$$\angle{ABD}=\alpha+\frac{\pi}{\mathrm{3}} \\ $$$${AB}=\frac{\mathrm{2}{R}\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{sin}\:\left(\alpha+\beta\right)×\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)} \\ $$$${s}=\frac{\mathrm{2}{R}\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta}{\mathrm{sin}\:\left(\alpha+\beta\right)×\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)} \\ $$$$\Rightarrow\lambda=\frac{{s}}{\mathrm{2}{R}}=\frac{\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta}{\mathrm{sin}\:\left(\alpha+\beta\right)×\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)}\:\:\:...\left({II}\right) \\ $$$${AE}=\mathrm{2}{R}\:\mathrm{cos}\:\beta \\ $$$${ED}=\mathrm{2}{R}\left[\mathrm{cos}\:\beta−\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)}\right] \\ $$$${EB}=\frac{\mathrm{2}{R}}{\mathrm{sin}\:\frac{\pi}{\mathrm{3}}}\left[\mathrm{cos}\:\beta−\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)}\right]\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow\frac{{EB}}{\mathrm{2}{R}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left[\mathrm{cos}\:\beta−\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)}\right]\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right) \\ $$$${EB}^{\mathrm{2}} =\left[\frac{\mathrm{2}{R}\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{sin}\:\left(\alpha+\beta\right)×\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)}\right]^{\mathrm{2}} +\left[\mathrm{2}{R}\:\mathrm{cos}\:\beta\right]^{\mathrm{2}} −\mathrm{2}×\frac{\mathrm{2}{R}\:\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{sin}\:\left(\alpha+\beta\right)×\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)}×\mathrm{2}{R}\:\mathrm{cos}\:\beta×\mathrm{cos}\:\beta \\ $$$$\left(\frac{{EB}}{\mathrm{2}{R}}\right)^{\mathrm{2}} =\left[\frac{\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{sin}\:\left(\alpha+\beta\right)×\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)}\right]^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \:\beta−\frac{\mathrm{2}\:\mathrm{sin}\:\alpha\:\mathrm{cos}^{\mathrm{2}} \:\beta\:\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{sin}\:\left(\alpha+\beta\right)×\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)} \\ $$$$\Rightarrow\left[\frac{\mathrm{sin}\:\alpha\:\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)\:\mathrm{sin}\:\left(\alpha+\beta\right)}\right]^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \:\beta−\frac{\mathrm{2}\:\mathrm{sin}\:\alpha\:\mathrm{cos}^{\mathrm{2}} \:\beta\:\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{sin}\:\left(\alpha+\frac{\pi}{\mathrm{3}}\right)\:\mathrm{sin}\:\left(\alpha+\beta\right)} \\ $$$$\:\:\:\:\:=\frac{\mathrm{4}}{\:\mathrm{3}}\left[\mathrm{cos}\:\beta\:\mathrm{sin}\:\left(\alpha+\beta\right)−\mathrm{sin}\:\alpha\right]^{\mathrm{2}} \left[\frac{\mathrm{sin}\:\left(\alpha+\beta+\frac{\pi}{\mathrm{3}}\right)}{\mathrm{sin}\:\left(\alpha+\beta\right)}\right]^{\mathrm{2}} \:\:\:...\left({I}\right) \\ $$$$ \\ $$$${we}\:{get}\:{from}\:\left({II}\right)\:{and}\:\left({I}\right)\:{graphically} \\ $$$$\lambda_{{max}} =\frac{{s}_{{max}} }{\mathrm{2}{R}}\approx\mathrm{0}.\mathrm{1831} \\ $$$${at}\:\alpha\approx\mathrm{16}.\mathrm{5}°\:{and}\:\beta\approx\mathrm{24}° \\ $$
Commented by mr W last updated on 28/Nov/20
Commented by ajfour last updated on 30/Nov/20
$${Thanks}\:{for}\:{solving}! \\ $$$${Marvellously}\:{done}. \\ $$