Among all triangles in the first quadrant formed by the x−axis, the y−axis and tangent lines to the graph of y = 3x−x^2 , what is the smallest possible area?


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 123817 by benjo_mathlover last updated on 28/Nov/20

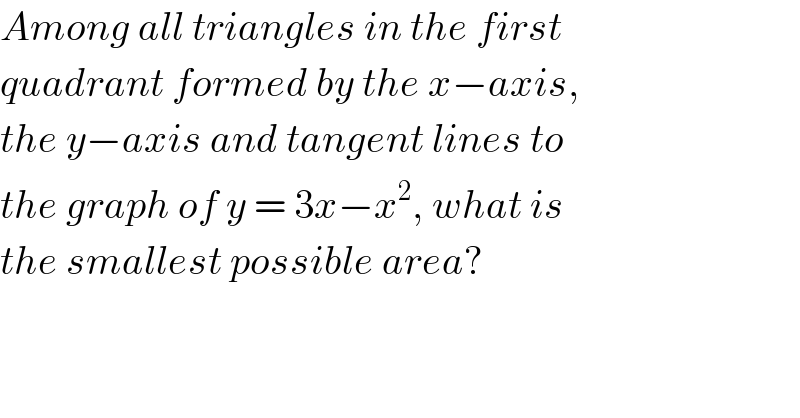
$A m o n g a l l t r i a n g l e s i n t h e f i r s t$ $q u a d r a n t f o r m e d b y t h e x - a x i s,$ $t h e y - a x i s a n d t a n g e n t l i n e s t o$ $t h e g r a p h o f y = 3 x - x^{2}, w h a t i s$ $t h e s m a l l e s t p o s s i b l e a r e a ?$
	Answered by MJS_new last updated on 28/Nov/20

	$since the curve includes the origin, the$ $smallest area is zero$
	Commented by benjo_mathlover last updated on 28/Nov/20

	$h a h a h a . . . n o s i r . b u t t h a n k y o u$
	Commented by MJS_new last updated on 28/Nov/20

	$I know the other one was meant but the$ $degenerated triangle A = B = C = (\begin{matrix} 0 \\ 0 \end{matrix}) is$ $there without a doubt . . . but of course {it}^{'} s$ $not the limit of the triangles in the 1^{st}$ $quadrant but in the 2^{nd} one .$
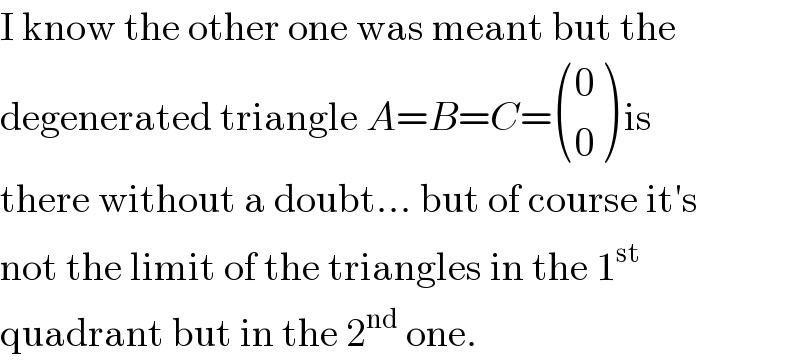
	Answered by mr W last updated on 28/Nov/20

	$t a n g e n t p o i n t P (p, y_{P})$ $y_{P} = 3 p - p^{2}$ $m = \frac{d y}{d x} = 3 - 2 x = 3 - 2 p$ $e q n . o f t a n g e n t :$ $y = m (x - p) + y_{P}$ $y = (3 - 2 p) x + p^{2}$ $\Rightarrow \frac{x}{\frac{p^{2}}{2 p - 3}} + \frac{y}{p^{2}} = 1$ $A r e a o f t r i a n g l e$ $A = \frac{p^{4}}{2 (2 p - 3)}$ $\frac{d (2 A)}{d p} = \frac{4 p^{3}}{2 p - 3} - \frac{2 p^{4}}{{(2 p - 3)}^{2}} = 0$ $p = 0 (r e j e c t e d) o r$ $\frac{p}{2 p - 3} = 2$ $\Rightarrow p = 2$ $\Rightarrow A_{m i n} = \frac{2^{4}}{2 (2 \times 2 - 3)} = 8$
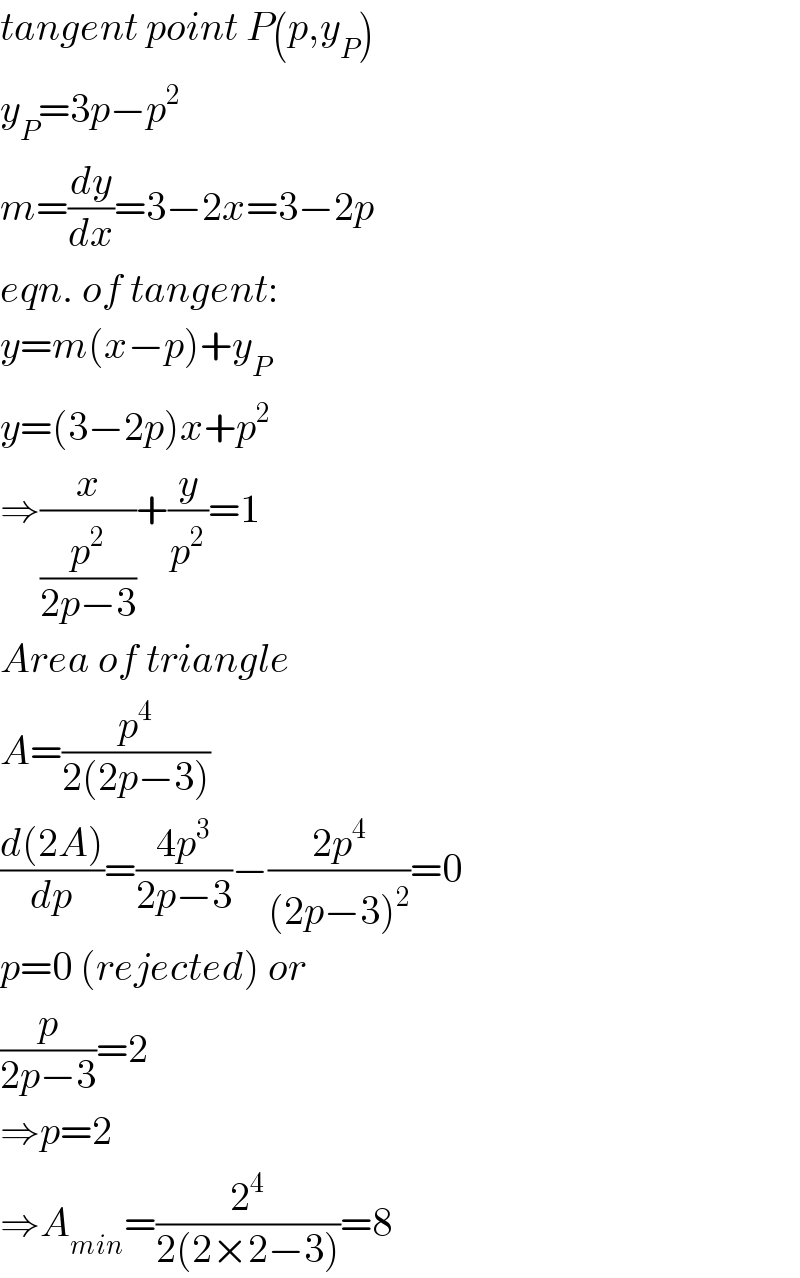
	Commented by mr W last updated on 28/Nov/20

	Commented by benjo_mathlover last updated on 28/Nov/20

	$y e s . . t h a n k y o u$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum